Формулы сокращенного умножения:
степень суммы и степень разности
Формулы сокращенного умножения включают в себя следующие группы формул:
 | Степень суммы |
 | Степень разности |
 | Квадрат многочлена |
 | Куб трехчлена |
 | Сумма нечетных степеней |
 | Разность нечетных степеней |
 | Разность четных степеней |
Степень суммы
Группа формул «Степень суммы» составляет Таблицу 1. Эти формулы можно получить, выполняя вычисления в следующем порядке:
| (x + y)2 = (x + y)(x + y) , (x + y)3 = (x + y)2(x + y) , (x + y)4 = (x + y)3(x + y) |
и т.д.
Группу формул «Степень суммы» можно получить также с помощью треугольника Паскаля и с помощью бинома Ньютона, которым посвящены специальные разделы нашего справочника.
Таблица 1. – Степень суммы
| Название формулы | Формула |
| Квадрат (вторая степень) суммы | (x + y)2 = x2 + 2xy + y2 |
| Куб (третья степень) суммы | (x + y)3 = x3 + 3x2y + 3xy2 + y3 |
| Четвертая степень суммы | (x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4 |
| Пятая степень суммы | (x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5 |
| Шестая степень суммы | (x + y)6 = x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 6xy5 + y6 |
| … | … |
Квадрат (вторая степень) суммы (x + y)2 = x2 + 2xy + y2 |
Куб (третья степень) суммы (x + y)3 = |
Четвертая степень суммы (x + y)4 = x4 + 4x3y + + 6x2y2 + 4xy3 + y4 |
Пятая степень суммы (x + y)5 = x5 + 5x4y + + 10x3y2 + + 10x2y3 + + 5xy4 + y5 |
Шестая степень суммы (x + y)6 = x6 + 6x5y + + 15x4y2 + + 20x3y3 + + 15x2y4 + 6xy5 + y6 |
| … |
Общая формула для вычисления суммы
(x + y)n
с произвольным натуральным значением n рассматривается в разделе «Бином Ньютона» нашего справочника.
Степень разности
Если в формулах из Таблицы 1 заменить y на – y , то мы получим группу формул «Степень разности» (Таблица 2.):
Таблица 2. – Степень разности
| Название формулы | Формула |
| Квадрат (вторая степень) разности | (x – y)2 = x2 – 2xy + y2 |
| Куб (третья степень) разности | (x – y)3 = x3 – 3x2y + 3xy2 – y3 |
| Четвертая степень разности | (x – y)4 = x4 – 4x3y + 6x2y2 – 4xy3 + y4 |
| Пятая степень разности | (x – y)5 = x5 – 5x4y + 10x3y2 – 10x2y3 + 5xy4– y5 |
| Шестая степень разности | (x – y)6 = x6 – 6x5y + 15x4y2 – 20x3y3 + 15x2y4 – 6xy5 + y6 |
| … | … |
Квадрат (вторая степень) разности (x – y)2 = x2 – 2xy + y2 |
Куб (третья степень) разности (x – y)3 = |
Четвертая степень разности (x – y)4 = x4 – 4x3y + + 6x2y2 – 4xy3 + y4 |
Пятая степень разности (x – y)5 = x5 – 5x4y + + 10x3y2 – – 10x2y3 + + 5xy4– y5 |
Шестая степень разности (x – y)6 = x6 – 6x5y + + 15x4y2 – – 20x3y3 + + 15x2y4 – 6xy5 + y6 |
| … |
Квадрат многочлена
Следующая формула применяется достаточно часто и называется «Квадрат многочлена»:
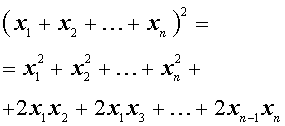
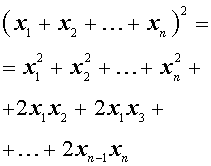
Словами эту формулу можно выразить так: - «Квадрат многочлена равен сумме квадратов всех его членов плюс сумма всевозможных удвоенных произведений его членов».
Куб трехчлена
Следующая формула называется «Куб трехчлена»:
= x3 + y3 + z3 + 3x2y +
+ 3x2z + 3xy2 +
+ 3xz2 +
+ 3y2z + 3yz2 + 6xyz .
Другие формулы сокращенного умножения приведены в разделе «Формулы сокращенного умножения: сумма степеней, разность степеней» нашего справочника.

| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
