Степень с целочисленным показателем и арифметический корень
 Степень с целочисленным показателем Степень с целочисленным показателем |
 Арифметический корень Арифметический корень |
 Избавление от иррациональностей в знаменателе дроби Избавление от иррациональностей в знаменателе дроби |
Степень с целочисленным показателем
Понятие степени с целочисленным показателем включает в себя три определения.
Определение. Пусть n – произвольное натуральное число, а a – произвольное действительное число. Тогда n – ой степенью числа a называют произведение n сомножителей, равных a :
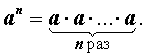
Число a называют основанием степени, а число n – показателем степени.
Определение. Пусть a – произвольное действительное число, отличное от 0 . Тогда, по определению:
a0 = 1 .
Число a называют основанием степени, а число 0 – показателем степени.
Определение. Пусть n – произвольное натуральное число, а a – произвольное действительное число, отличное от 0 . Тогда, по определению:
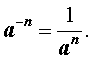
Число a называют основанием степени, а число (– n) – показателем степени.
Таким образом, степень с целочисленным показателем определена.
Пример 1.
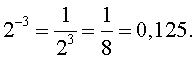
Замечание 1. Число нуль нельзя возвести в нулевую степень и нельзя возвести в отрицательную степень.
Арифметический корень
Пусть n – произвольное натуральное число, а a – произвольное положительное число.
Определение. Число x называют арифметическим корнем n – ой степени из числа a , если, во-первых, число x положительное, а, во-вторых, является решением уравнения
xn = a .
В этом случае при ![]() для арифметического корня используется обозначение:
для арифметического корня используется обозначение:
![]()
или эквивалентное обозначение:
![]()
Если же n = 2, то для арифметического квадратного корня используется обозначение:
![]()
или эквивалентное обозначение:
![]()
Замечание 2. В курсах математики, выходящих за рамки средней школы, доказывается, что арифметический корень всегда существует, причем только один.
Замечание 3. Очень важно помнить о том, что в формуле
![]()
содержится ошибка, за которую мгновенно следует безжалостная кара на экзаменах.
Пример 2. Решить уравнение
x2 = 25 .
Решение. Это уравнение имеет два корня:
x1 = 5 и x2 = – 5 .
Корень уравнения x1 = 5 является арифметическим квадратным корнем из числа 25, а корень уравнения x2 = – 5 является числом, противоположным к арифметическому квадратному корню из числа 25.
Пример 3. Решить уравнение
x3 = – 27 .
Решение. Это уравнение имеет единственный вещественный корень x = – 3, но это число не является арифметическим кубическим корнем из числа (– 27), так как у отрицательных чисел не бывает арифметических корней. Число x = – 3 является числом, противоположным к арифметическому кубическому корню из числа 27. Поэтому
![]()
Замечание 4. Желающие могут ознакомиться с нашей презентацией «Степень с рациональным показателем», содержание которой связано с данным разделом.
Избавление от иррациональностей в знаменателе дроби
В некоторых задачах требуется перейти от дроби к равной ей дроби, но такой, у которой в знаменателе нет корней (иррациональностей). Эта операция носит название «избавление от иррациональностей в знаменателе дроби» и осуществляется при помощи умножения числителя и знаменателя дроби на подходящее число. Часто это число находится с помощью формул сокращенного умножения. Покажем это на примере.
Пример 4. Преобразовать дробь
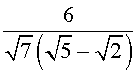
к такому виду, чтобы в знаменателе не было иррациональностей.
Решение. Воспользовавшись формулой сокращенного умножения «Разность квадратов», совершим следующие эквивалентные преобразования:
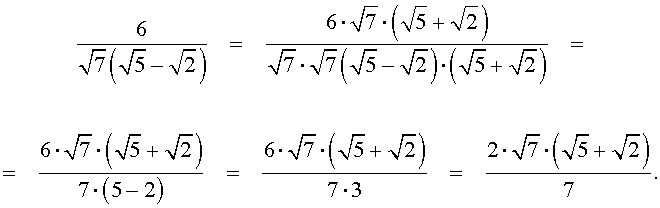
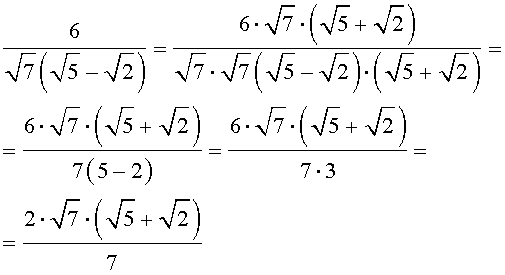
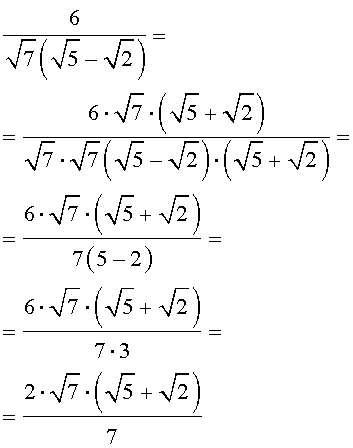
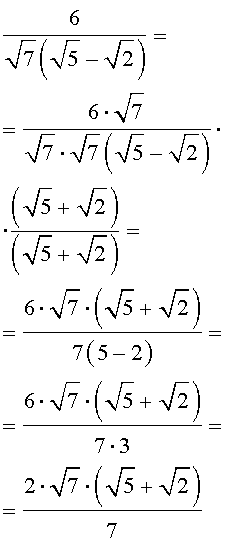
Мы получили дробь, у которой в знаменателе иррациональностей нет, что и требовалось.
С понятием степени с рациональным показателем и свойствами степеней можно ознакомиться в разделе «Степень с рациональным показателем» нашего справочника.
Графики степенных и показательных функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.

На сайте можно также ознакомиться с нашимиучебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ОГЭ по математике осталось | |||
| дней | часов | минут | секунд |
