Линейные уравнения и неравенства
 Линейные уравнения |
| Линейные неравенства |
| Системы линейных неравенств |
Линейные уравнения
Линейным уравнением относительно переменной x называется уравнение первой степени
| kx + b = 0 , | (1) |
где k и b – произвольные вещественные числа.
В случае 
уравнение (1) имеет единственное решение при любом значении b :
В случае, когда 
уравнение (1) решений не имеет.
В случае, когда k = 0, b = 0, решением уравнения (1) является любое число
Линейные неравенства
Линейным неравенством относительно переменной x называется неравенство, принадлежащее к одному из следующих типов:
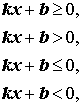
где k и b – произвольные вещественные числа.
Решая линейные, да и не только линейные, неравенства, следует помнить, что
| при умножении или делении неравенства на положительное число знак неравенства сохраняется, |
а
| при умножении или делении неравенства на отрицательное число знак неравенства меняется на противоположный. |
В соответствии с этим решение линейных неравенств, в зависимости от значений коэффициентов k и b, представлено в следующей Таблице 1.
Таблица 1. – Решение неравенств первой степени (линейных неравенств)
 | kx + b > 0 |  | kx + b < 0 | |
| k > 0 | Знак неравенства сохраняется | |||
 |  |  |  | |
| k = 0, b < 0 |  | | | |
| k = 0, b = 0 | | | | |
| k = 0, b > 0 | | | | |
| k < 0 | Знак неравенства меняется на противоположный | |||
 |  |  |  | |
| kx + b > 0 | | kx + b < 0 |
| k > 0 Знак неравенства сохраняется | |||
| | | |
| k = 0, b < 0 | |||
| | | |
| k = 0, b = 0 | |||
| | | |
| k = 0, b > 0 | |||
| | | |
| k < 0 Знак неравенства меняется на противоположный | |||
| | | |
| k > 0 Знак неравенства сохраняется |
Неравенство:
Решение неравенства:
|
Неравенство: kx + b > 0 Решение неравенства:
|
Неравенство:
Решение неравенства:
|
Неравенство: kx + b < 0 Решение неравенства:
|
| k = 0, b < 0 |
Неравенство:
Решение неравенства:
|
Неравенство: kx + b > 0 Решение неравенства:
|
Неравенство:
Решение неравенства:
|
Неравенство: kx + b < 0 Решение неравенства:
|
| k = 0, b = 0 |
Неравенство:
Решение неравенства:
|
Неравенство: kx + b > 0 Решение неравенства:
|
Неравенство:
Решение неравенства:
|
Неравенство: kx + b < 0 Решение неравенства:
|
| k = 0, b > 0 |
Неравенство:
Решение неравенства:
|
Неравенство: kx + b > 0 Решение неравенства:
|
Неравенство:
Решение неравенства:
|
Неравенство: kx + b < 0 Решение неравенства:
|
| k < 0 Знак неравенства меняется на противоположный |
Неравенство:
Решение неравенства:
|
Неравенство: kx + b > 0 Решение неравенства:
|
Неравенство:
Решение неравенства:
|
Неравенство: kx + b < 0 Решение неравенства:
|
Системы линейных неравенств
Рассмотрим решение систем линейных неравенств на примерах.
Пример 1. Решить систему неравенств
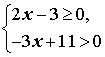
Решение. Решим каждое из неравенств системы:
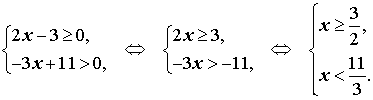
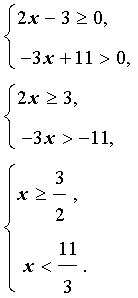
Изобразив на одной координатной прямой (рис. 1) оба точечных множества, составляющих последнюю систему, получаем ответ примера.
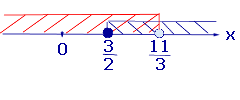
Рис.1
Ответ: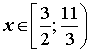 
Пример 2. Решить систему неравенств
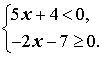
Решение. Решим каждое из неравенств системы:
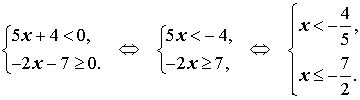
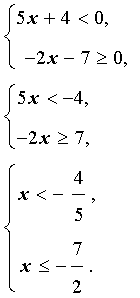
Изобразив на одной координатной прямой (рис. 2) оба точечных множества, составляющих последнюю систему, получаем ответ примера.
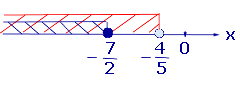
Рис.2
Ответ: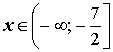 
Пример 3. Решить систему неравенств
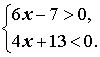
Решение. Решим каждое из неравенств системы:
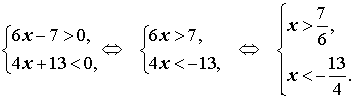
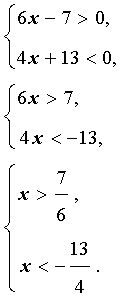
Изобразив на одной координатной прямой (рис. 3) оба точечных множества, составляющих последнюю систему, получаем ответ примера
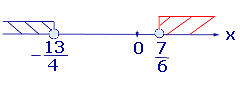
Рис.3
Ответ:
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |