Средние значения
Обозначим буквой p произвольное действительное число и рассмотрим произвольный набор из n положительных действительных чисел
x1 , x2 , … , xn
( n – натуральное число).
Определение. Средним значением степени p для набора чисел
x1 , x2 , … , xn
называют величину, определяемую формулой
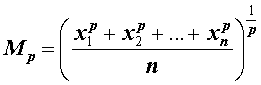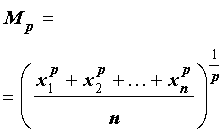  | (1) |
В случае, когда p = 1 , среднее значение степени 1 имеет вид
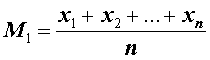
и называется средним арифметическим n чисел.
Таким образом, среднее арифметическое n чисел равно сумме этих чисел, деленной на n .
В случае, когда p = 2 , среднее значение степени 2 имеет вид
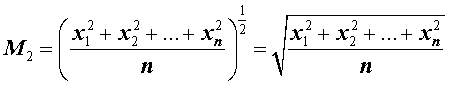
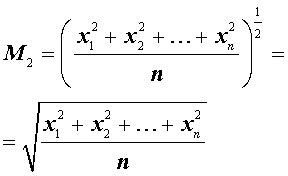
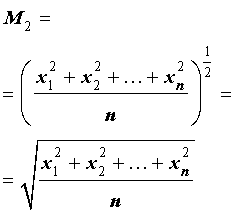
и называется средним квадратичным (средним квадратическим) n чисел.
Другими словами, среднее квадратичное n чисел равно квадратному корню из среднего арифметического квадратов этих чисел.
В случае, когда p = – 1, среднее значение степени (– 1) имеет вид
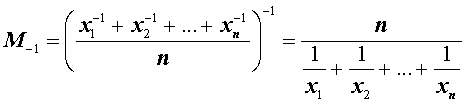
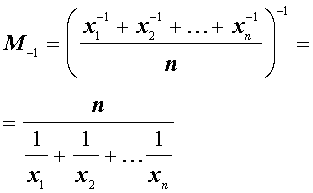
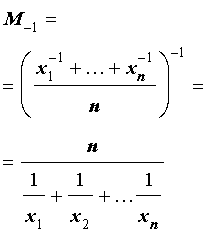
и называется средним гармоническим n чисел.
Итак, среднее гармоническое n чисел равно обратной величине от среднего арифметического обратных величин этих чисел.
Поскольку на нуль делить нельзя, то и использовать формулу (1) для определения среднего значения степени 0 нельзя. Однако среднее значение степени 0 можно получить, если в формуле (1) осуществить предельный переход при 
. Не останавливаясь на доказательстве корректности такого предельного перехода, приведем только окончательный результат.
Утверждение. При p = 0 среднее значение степени 0 вычисляется по формуле:
Определение. Среднее значение степени 0 называется средним геометрическим (средним пропорциональным) n чисел.
В соответствии с приведенной выше формулой среднее геометрическое n чисел равно корню n – ой степени из произведения этих чисел.
Если в формуле (1) совершить предельный переход при 
, то мы получим среднее значение степени 
, причем
Другими словами, среднее значение степени из n чисел равно наибольшему из этих чисел.
Если же в формуле (1) совершить предельный переход при 
, то мы получим среднее значение степени 
, причем
Таким образом, среднее значение степени из n чисел равно наименьшему из этих чисел.
Для удобства сформируем Таблицу из определений средних значений:
Таблица – Средние значения
| Обозначение | Формула | Название |
 | min ( x1 , x2 , … , xn ) | Минимум |
| M– 1 | 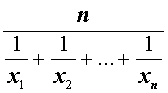 | Среднее гармоническое |
| M0 |  | Среднее геометрическое |
| M1 | 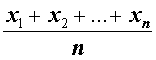 | Среднее арифметическое |
| M2 | 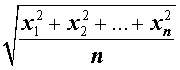 | Среднее квадратичное |
 | max ( x1 , x2 , … , xn ) | Максимум |
| Минимум |
Обозначение:
Формула: min ( x1 , x2 , … , xn ) |
| Среднее гармоническое |
Обозначение: M– 1 Формула:
|
| Среднее геометрическое |
Обозначение: M0 Формула:
|
| Среднее арифметическое |
Обозначение: M1 Формула:
|
| Среднее квадратичное |
Обозначение: M2 Формула:
|
| Максимум |
Обозначение:
Формула: max ( x1 , x2 , … , xn ) |
Неравенства между средними значениями для одного и того же набора чисел приведены в разделе «Неравенства между средними значениями» нашего справочника.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
| ||||||
| ||||||
