Справочник по математике

Алгебра

Средние значения

Неравенства между средними значениями

Неравенства между средними значениями

Неравенство Коши о среднем арифметическом и среднем геометрическом

Неравенство о среднем гармоническом и среднем геометрическом

Неравенство о среднем квадратичном и среднем арифметическом

Неравенства между средними значениями

      Для удобства приведем Таблицу из введенных в разделе «Средние значения» определений средних значений для произвольного набора из   n   положительных действительных чисел

x₁ ,  x₂ , … , x_n

      Таблица – Средние значения

Обозначение	Формула	Название
	min ( x1 ,  x2 , … , xn )	Минимум
M– 1		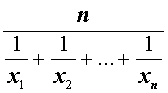Среднее гармоническое
M0		Среднее геометрическое
M1		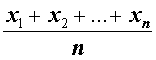Среднее арифметическое
M2		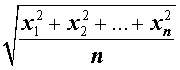Среднее квадратичное
	max ( x1 ,  x2 , … , xn )	Максимум

      Утверждение 1. Пусть   p₁   и   p₂   – произвольные действительные числа, удовлетворяющие неравенству   p₁< p₂ .   Тогда для произвольного набора из   n   положительных действительных чисел

x₁ ,  x₂ , … , x_n

справедливо неравенство

,

причем в этом неравенстве знак равенства выполняется тогда и только тогда, когда все числа

x₁ ,  x₂ , … , x_n

равны.

      Замечание. Утверждение 1 остается справедливым и в случае, когда , и в случае, когда.

      Следствие 1. Для произвольного набора из   n   положительных чисел

x₁ ,  x₂ , … , x_n

справедливы следующие неравенства между его средними значениями:

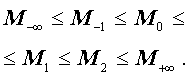
      Следствие 2. Для произвольного набора из   n   положительных чисел

x₁ ,  x₂ , … , x_n

любые два из его средних значений

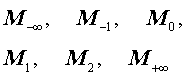
равны между собой тогда и только тогда, когда все числа

x₁ ,  x₂ , … , x_n

равны.

      Итак, для   n   произвольных положительных чисел

x₁ ,  x₂ , … , x_n

справедлива следующая цепочка неравенств:

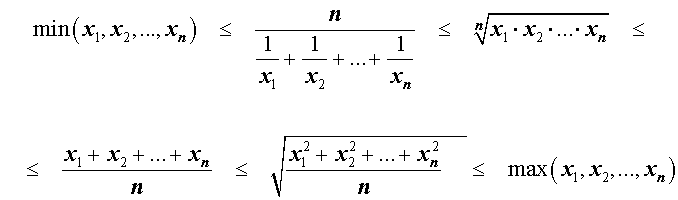
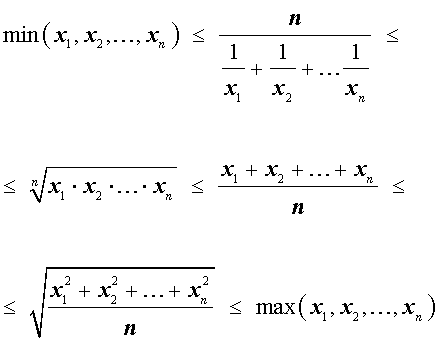
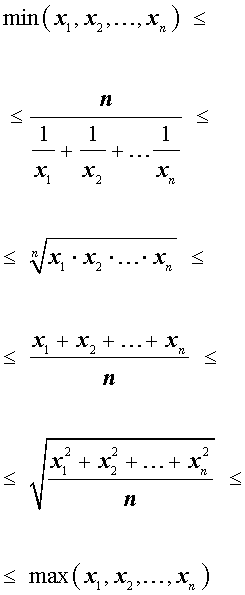
Неравенство Коши о среднем арифметическом и среднем геометрическом

      Неравенство

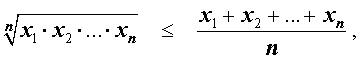
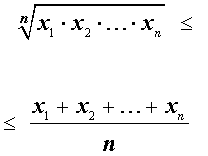
утверждающее, что среднее геометрическое   n   положительных чисел не превосходит их среднего арифметического, называется неравенством Коши.

      В случае, когда   n = 2 ,   неравенство Коши имеет вид

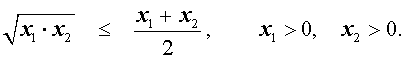
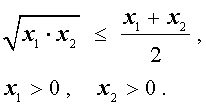
      Докажем это неравенство:

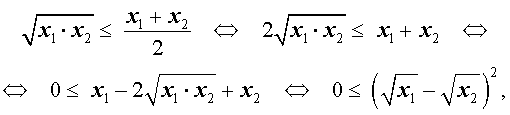
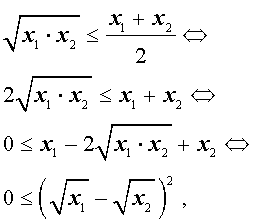
что и требовалось.

     Из неравенства Коши с   n = 2 ,   взяв

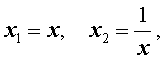
нетрудно получить очень полезное следствие.

      Следствие. Для произвольного положительного числа   x   выполнено неравенство

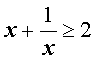
Неравенство о среднем гармоническом и среднем геометрическом

      В случае   n   переменных неравенство о среднем гармоническом и среднем геометрическом имеет вид:

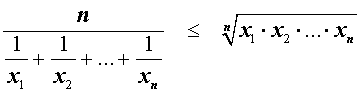
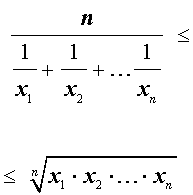
      В случае, когда   n = 2 ,   это неравенство имеет вид:

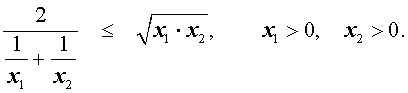
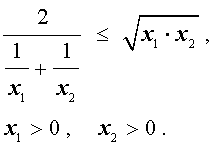
      Докажем это неравенство:

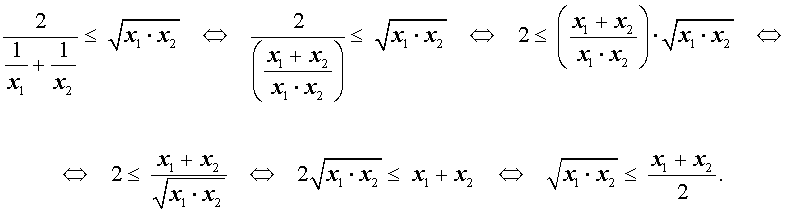
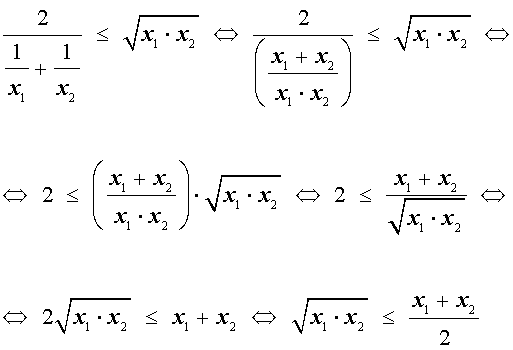
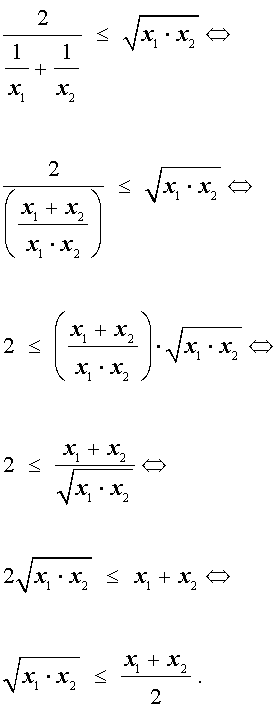
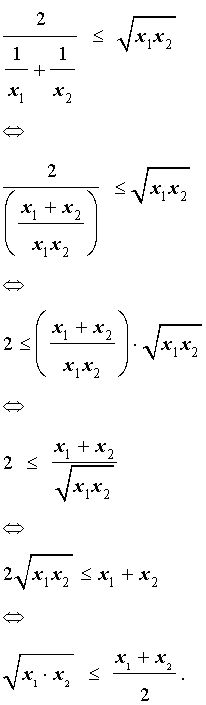
      На последнем этапе получилось неравенство Коши, доказанное в предыдущем разделе, следовательно, доказательство неравенства о среднем гармоническом и среднем геометрическом закончено.

Неравенство о среднем квадратичном и среднем арифметическом

      В случае   n   переменных неравенство о среднем квадратичном и среднем арифметическом имеет вид:

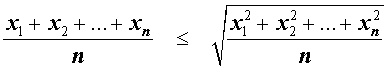
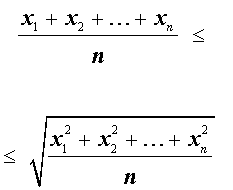
      В случае, когда   n = 2 ,   это неравенство имеет вид:

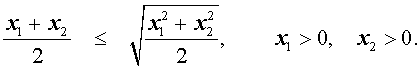
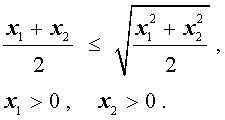
      Докажем это неравенство:

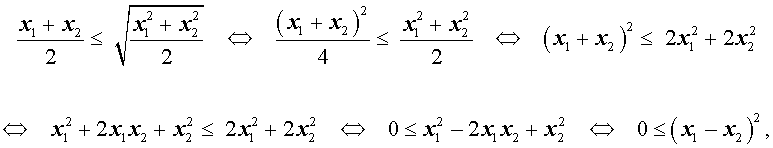
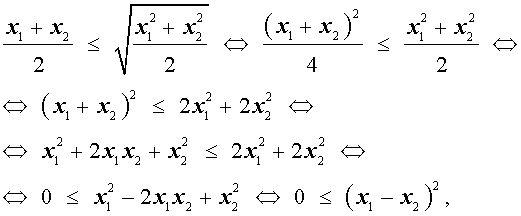
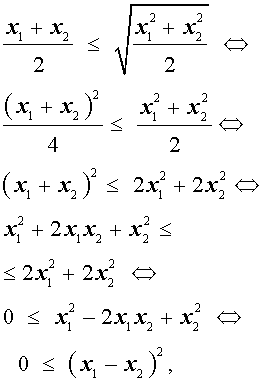
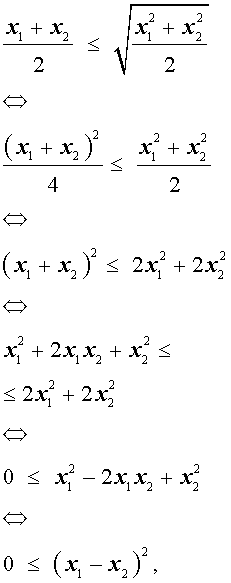
что и требовалось.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.