Вневписанные окружности
Теорема 1. В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.
Доказательство. Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).
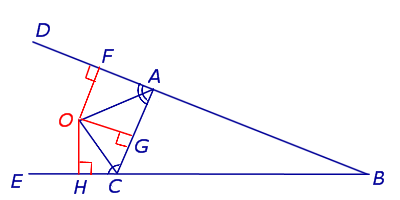
Рис.1
Проведём биссектрисы углов DAC и ECA, которые являются внешними углами треугольника ABC. Обозначим точку пересечения этих биссектрис буквой O. Докажем, что точка O лежит на биссектрисе угла ABC, который является внутренним углом треугольника ABC, не смежным с внешними углами DAC и ECA. С этой целью опустим из точки O перпендикуляры OF, OG и OH на прямые AB, AC и BC соответственно. Поскольку AO – биссектриса угла DAC, то справедливо равенство:
OF = OG,
Поскольку CO – биссектриса угла ACE, то справедливо равенство:
OF = OG,
Следовательно, справедливо равенство
OG = OH,
откуда вытекает, что точка O лежит на биссектрисе угла ABC, что и требовалось доказать.
Замечание 1. В ходе доказательства теоремы 1 мы установили, что справедливы равенства
OF = OG = OH,
откуда вытекает, что точки F,G и H лежат на одной окружности с центром в точке O.
Определение. Окружность называют окружностью, вневписанной в треугольник, или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).
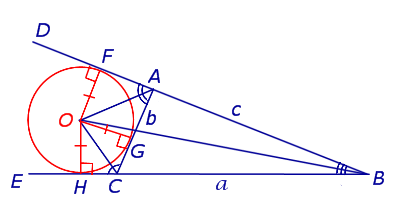
Рис.2
Замечание 2. У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.
Замечание 3. Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B, а окружность касается стороны b. Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b, и обозначать её радиус символом rb .
Теорема 2. Пусть вневписанная окружность касается стороны AC треугольника ABC. Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.
Доказательство. Снова рассмотрим рисунок 2 и докажем, что выполнено равенство
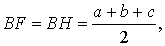
где a, b, c – стороны треугольника ABC. Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A. Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C. Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B. Отсюда получаем:
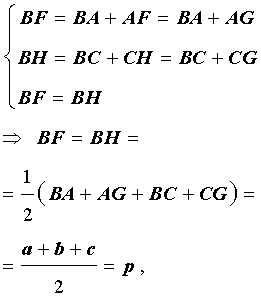
где буквой p обозначен полупериметр треугольника ABC. Теорема 2 доказана.
Теорема 3. Радиус вневписанной окружности, касающейся стороны b, вычисляется по формуле
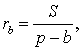
где буквой S обозначена площадь треугольника ABC, а буквой p обозначен полупериметр треугольника ABC.
Доказательство. Снова рассмотрим рисунок 2 и заметим, что выполнены равенства
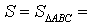
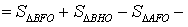
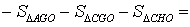
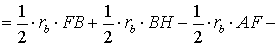
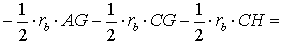
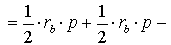
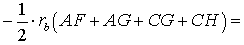
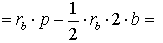
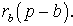
Следовательно, справедливо равенство
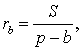
что и требовалось доказать.
Следствие. Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:
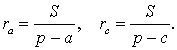
Теорема 4. Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:
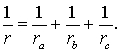
Доказательство. Поскольку
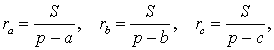
то
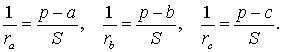
Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности
,
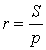получим
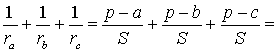
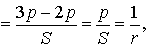
что и требовалось доказать.
Теорема 5. Площадь треугольника можно вычислить по формуле
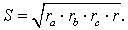
Доказательство. Перемножим формулы
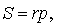
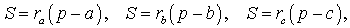
и воспользуемся формулой Герона:
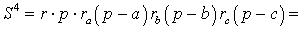
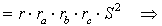
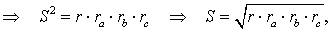
что и требовалось доказать.
Теорема 6. Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:
ra + rb + rc – r = 4R .
Доказательство. Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим
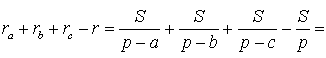
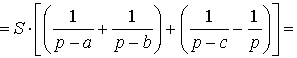
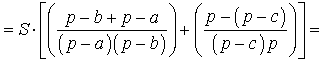
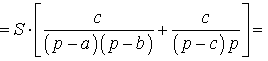
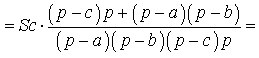
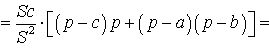
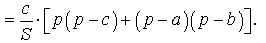
Преобразуем выражение, стоящее в квадратной скобке:
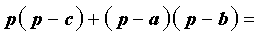
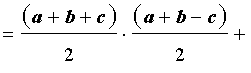
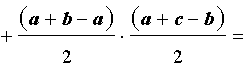
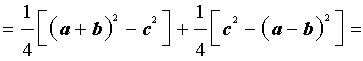
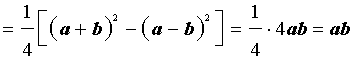
В результате получаем равенство
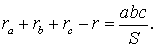
Поскольку радиус описанной окружности удовлетворяет равенству
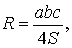
то справедлива формула
ra + rb + rc – r = 4R ,
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |