Справочник по математике Тригонометрия
Тригонометрия
Тригонометрические функции произвольного угла
Содержание
 |
Определение тригонометрических функций произвольного угла |
 |
Основное тригонометрическое тождество. Тригонометрический круг |

Определение тригонометрических функций произвольного угла
Рассмотрим окружность радиуса R с центром в начале прямоугольной системой координат Oxy.
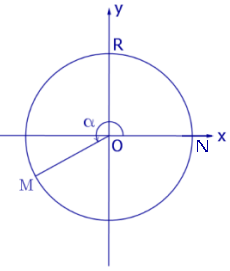
Рис.1
Положительным считается угол NOM, сторона OM которого получена из положительной полуоси Ox в результате поворота, осуществляемого в направлении движения против часовой стрелки (рис.1).
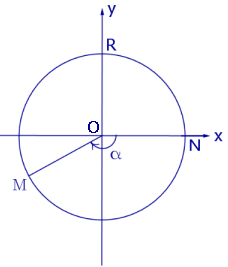
Рис.2
Отрицательным считается угол NOM, сторона OM которого получена из положительной полуоси Ox в результате поворота, осуществляемого в направлении, совпадающем с направлением движения часовой стрелки (рис. 2).
Если для координат точки M0 , лежащей на окружности радиуса R с центром в начале координат O (рис. 3),
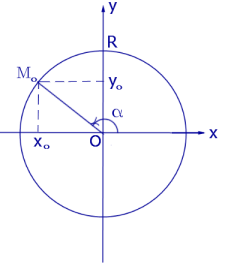
Рис.3
ввести обозначение
M0 = ( x0 ; y0 ),
то, в силу теоремы Пифагора, будет справедливо равенство:
x02 + y02 = R2,
и можно сформулировать следующее общее определение тригонометрических функций произвольного угла.
Синусом, косинусом, тангенсом и котангенсом произвольного угла α называют числа, определяемые по формулам:
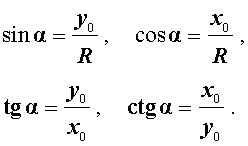
ЗАМЕЧАНИЕ 1. Отметим следующее важное свойство тригонометрических функций синуса и косинуса произвольного угла:
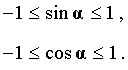
ЗАМЕЧАНИЕ 2. Определение тригонометрических функций произвольного угла является естественным обобщением определения тригонометрических функций острого угла, данного в разделе справочника "Тригонометрические функции острого угла".
Основное тригонометрическое тождество. Тригонометрический круг
Рассмотрим окружность радиуса 1 с центром в начале координат. Если для координат точки M1 (рис. 4), лежащей на этой окружности,
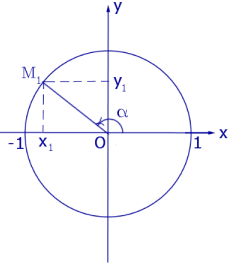
Рис.4
ввести обозначение
M1 = ( x1 ; y1 ) ,
то, в силу теоремы Пифагора, будет справедливо равенство
x12 + y12 = 1 ,
а синус, косинус, тангенс и котангенс угла α будут вычисляться по формулам
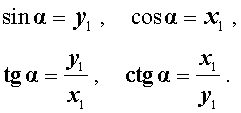
Из этих формул, в частности, вытекает основное тригонометрическое тождество:
sin2α + cos2α = 1 .
Таким образом, основное тригонометрическое тождество является теоремой Пифагора, сформулированной с помощью тригонометрических функций.
Окружность радиуса 1, изображенную на рисунке 4, называют тригонометрическим кругом или числовой окружностью.
