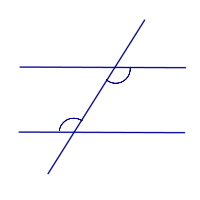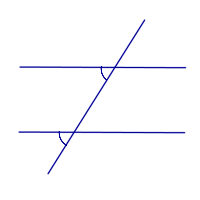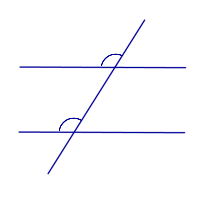Справочник по математике

Геометрия (Планиметрия)

Параллельность прямых

Признаки параллельности прямых

      При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.

Углы, образующиеся при пересечении двух прямых третьей прямой

Рисунок	Определение углов
	Внутренние накрест лежащие углы
	Внешние накрест лежащие углы
	Соответственные углы
	Внутренние односторонние углы
	Внешние односторонние углы

Внутренние накрест лежащие углы

Внешние накрест лежащие углы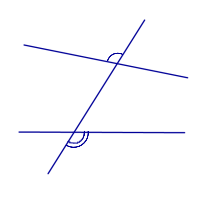

Соответственные углы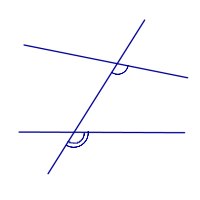

Внутренние односторонние углы

Внешние односторонние углы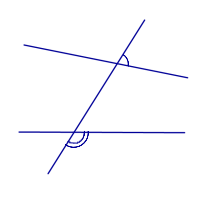

      Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.

      Определение. Две прямые на плоскости называются параллельными, если они не имеют общих точек.

     Замечание. Два отрезка называются параллельными, если они лежат на параллельных прямых.

Признаки параллельности двух прямых

Рисунок	Признак параллельности
	Прямые параллельны тогда и только тогда, когда внутренние накрест лежащие углы  равны
	Прямые параллельны тогда и только тогда, когда внешние накрест лежащие углы равны
	Прямые параллельны тогда и только тогда, когда соответственные углы равны
	Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна180°
	Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Следствие

Рисунок	Признак параллельности
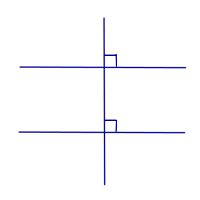
	Две прямые, перпендикулярные к третьей прямой, параллельны

Переход свойства параллельности прямых

Рисунок	Признак параллельности
	Если прямая a параллельна прямой b, а прямая b параллельна прямой c, то прямая a параллельна прямой c

      Задача. Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.

      Решение. Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.