Рациональные корни многочленов с целыми коэффициентами
Прежде, чем дать общую формулировку теоремы о рациональных корнях многочленов с целыми коэффициентами, решим следующую задачу.
Задача. Найти все корни уравнения
являющиеся рациональными числами.
Решение. Предположим, что рассматриваемое уравнение имеет корень, являющийся рациональным числом. Тогда, поскольку каждое рациональное число можно представить в виде несократимой дроби
,
где 
– число целое, а 
– число натуральное, то выполняется равенство:
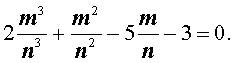
Умножая это равенство на 
, получаем равенство:
 |
(1) |
Теперь преобразуем равенство (1):
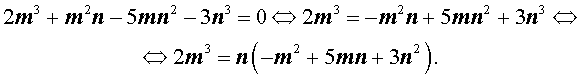
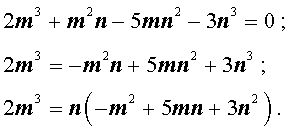
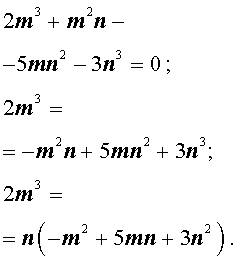
Отсюда вытекает, что число 
нацело делится на число . А из этого, в свою очередь, следует, что, поскольку числа и не имеют общих простых делителей, то число является делителем числа 2. Таким образом, число равно 1 или 2.
Теперь преобразуем равенство (1) по-другому:
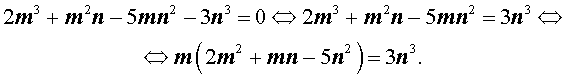
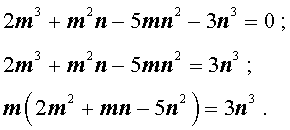
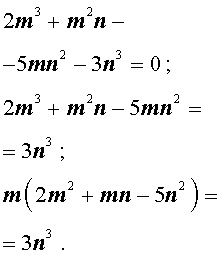
Значит, число 
нацело делится на число . А из этого, в свою очередь, следует, что, так как числа и не имеют общих простых делителей, то число является делителем числа 3. Таким образом, число может быть равно: -1,1,-3 или 3.
Далее, рассматривая все возможные комбинации чисел и , получаем, что дробь
может принимать только следующие значения:
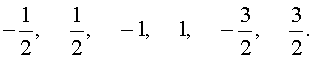
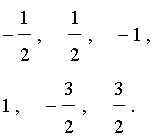
Таким образом, если у исходного уравнения и есть рациональный корень, то искать его нужно среди полученных шести чисел. Других рациональных корней у исходного уравнения быть не может.
Подставляя поочередно каждое из этих чисел в исходное уравнение, получаем, что корнем уравнения является лишь число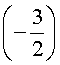 
.
Оставляя читателю проверку того, что другие числа корнями исходного уравнения не являются, покажем, что число 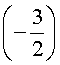действительно является его корнем:
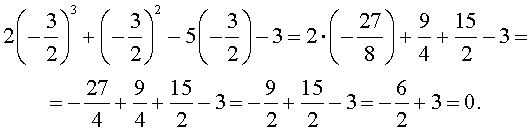
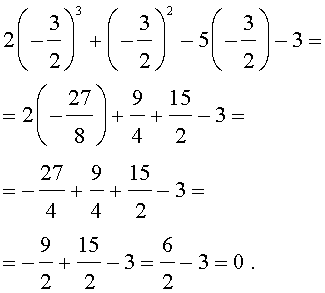
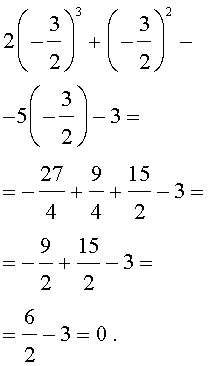
Ответ. Число 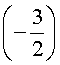является единственным рациональным корнем исходного уравнения.
Замечание. Для того, чтобы найти все остальные корни исходного уравнения, нужно, воспользовавшись теоремой Безу, разделить многочлен
на двучлен
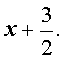
В результате деления получится квадратный трехчлен
после чего остается лишь решить квадратное уравнение:
Теорема. Если рациональное число (несократимая дробь)
,
где – число целое, а – число натуральное, является корнем многочлена 
-ой степени
все коэффициенты
которого являются целыми числами, то числитель дроби является делителем коэффициента 
, а знаменатель дроби является делителем коэффициента 
.
Коэффициент называют старшим коэффициентом многочлена, а коэффициент - свободным членом многочлена.
Алгебраические и трансцендентные числа
Определение. Действительное число называют действительным алгебраическим числом, если существует многочлен с целочисленными коэффициентами, корнем которого это число является. Если же такой многочлен не существует, то указанное число называют действительным трансцендентным числом.
Замечание. Числа 
и 
– наиболее известные примеры действительных трансцендентных чисел.
Утверждение. Каждое рациональное число является алгебраическим числом.
Доказательство. Каждое рациональное число представимо в виде несократимой дроби
,
где – число целое, а – число натуральное. Но указанная дробь является корнем уравнения первой степени
что и требовалось доказать.
Следствие. Каждое действительное трансцендентное число является иррациональным числом.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра "Резольвента" учебными материалами для подготовки к ЕГЭ и ГИА по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика "проблемными".
Запись по телефону (495) 509-28-10. |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ГИА по математике, физике или русскому языку на высокий балл, учебный центр "Резольвента"
проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр "РЕЗОЛЬВЕНТА"
