Решение кубических уравнений. Формула Кардано
Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени (кубических уравнений)
| a0x3 + a1x2 + + a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа, ![]()
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями.
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x3 + ax2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
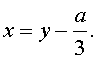 | (3) |
Тогда, поскольку
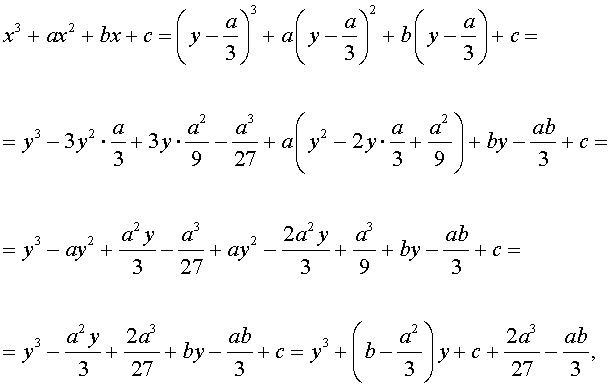
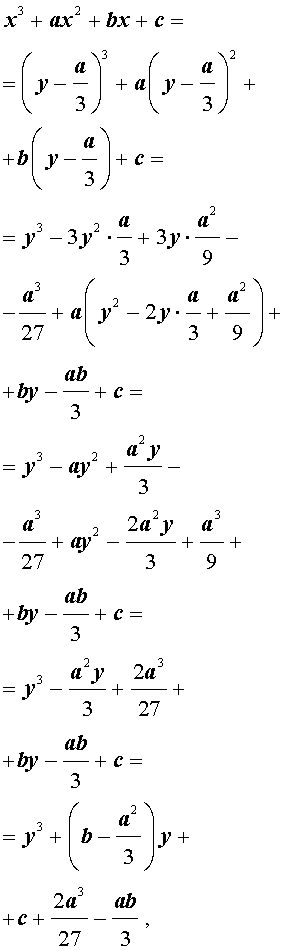
то уравнение (2) примет вид
В результате уравнение (2) примет вид
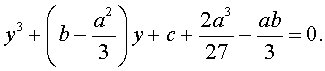 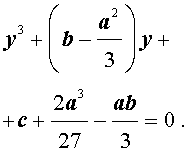 | (4) |
Если ввести обозначения
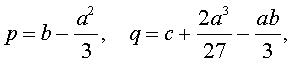
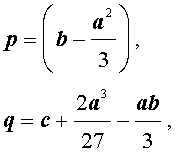
то уравнение (4) примет вид
| y3 + py + q= 0, | (5) |
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями, у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
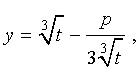 | (6) |
где t – новая переменная.
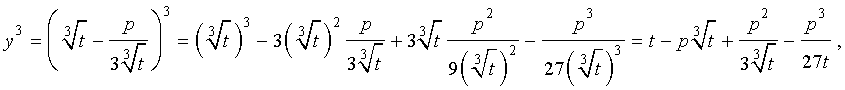
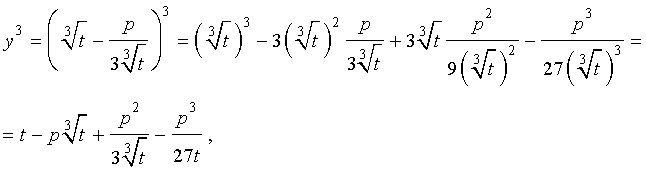
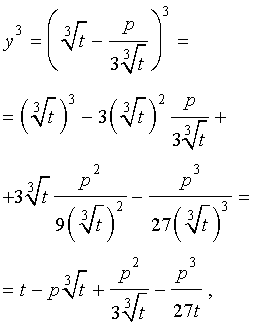
то выполнено равенство:
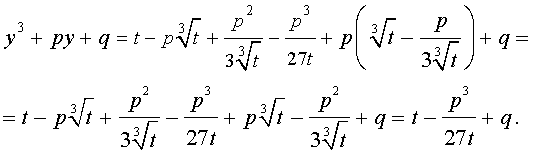
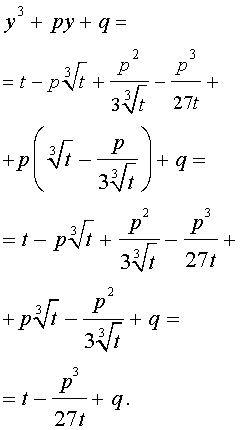
Следовательно, уравнение (5) переписывается в виде
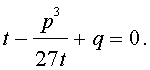 | (7) |
Если теперь уравнение (7) умножить на t, то мы получим квадратное уравнение относительно t :
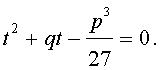 | (8) |
Формула Кардано
Решение уравнения (8) имеет вид:
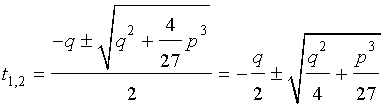
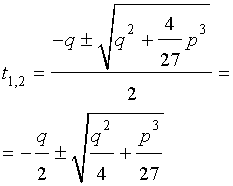
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
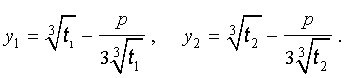 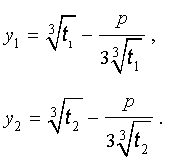 | (9) |
В развернутой форме эти решения записываются так:
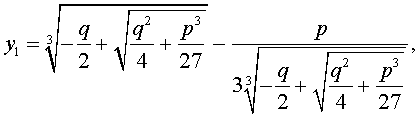 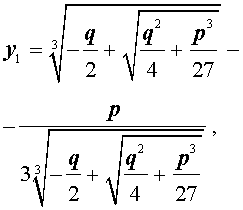 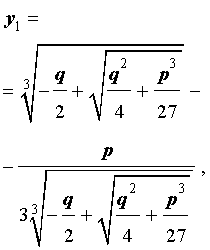 | (10) |
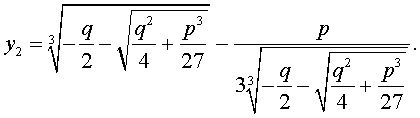 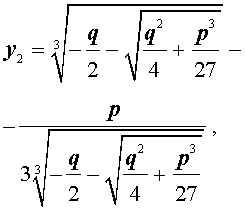 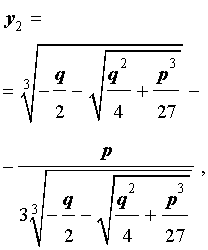 | (11) |
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
Действительно,
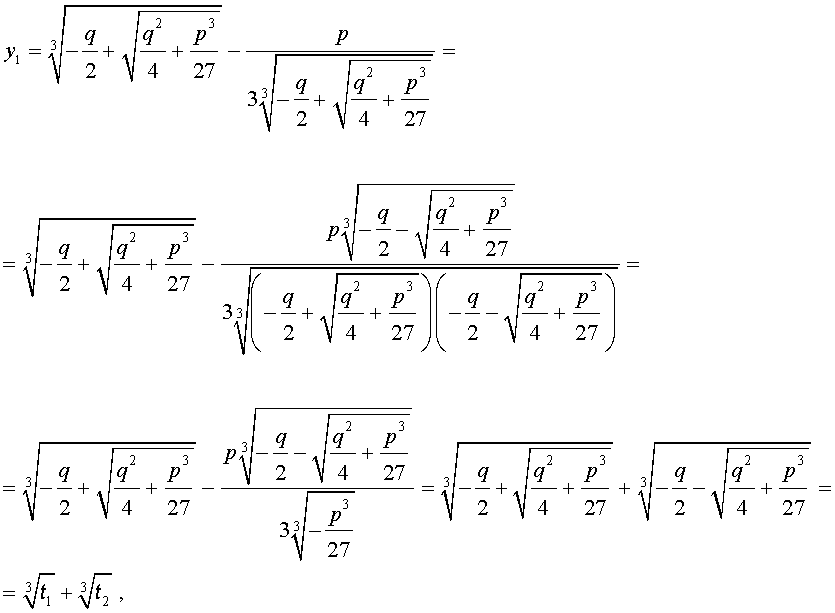
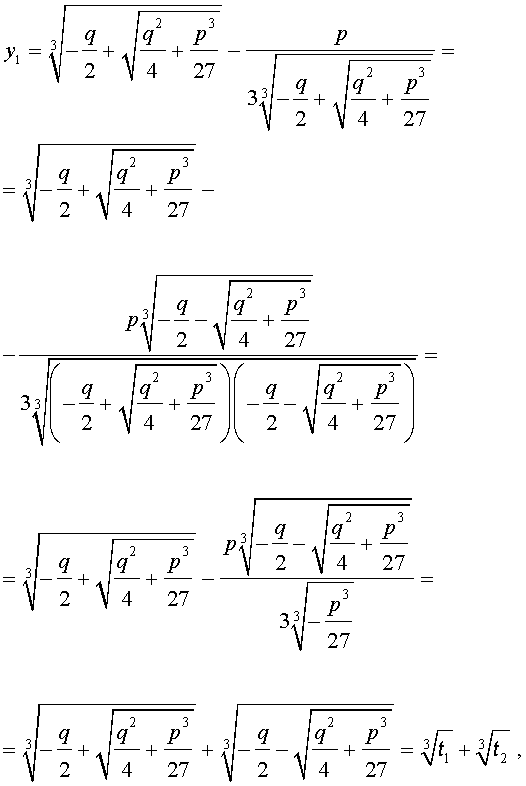

С другой стороны,
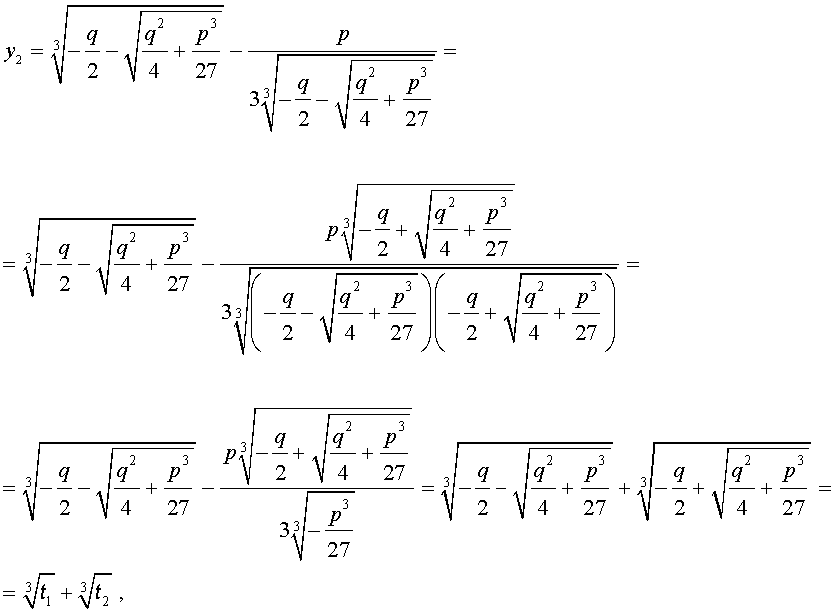
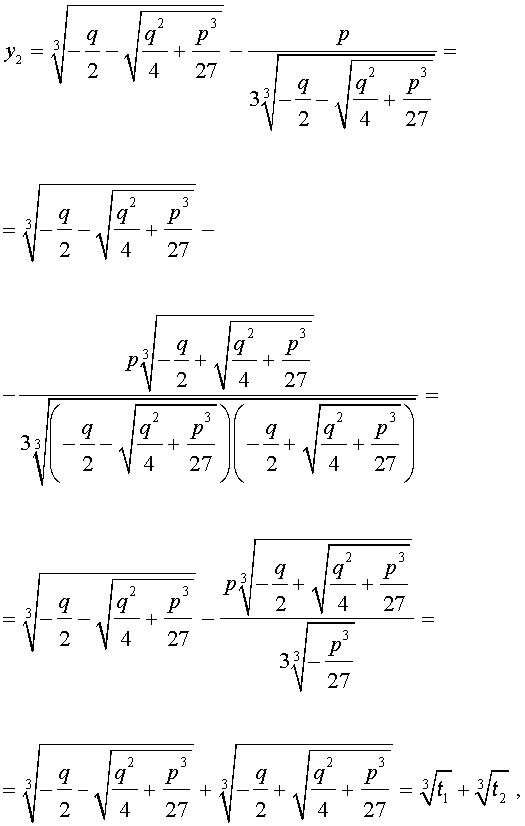

Таким образом,
![]()
и для решения уравнения (5) мы получили формулу
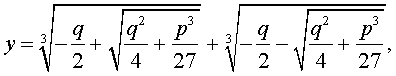 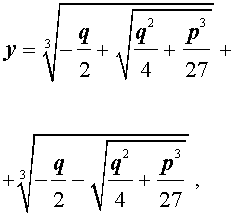 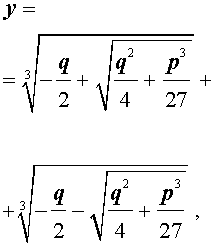 | (12) |
которая и называется «Формула Кардано».
Замечание. Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Пример решения кубического уравнения
Пример. Решить уравнение
| x3 – 6x2 – 6x – 2 = 0. | (13) |
Решение. Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
| x = y + 2. | (14) |
Тогда получим
= (y + 2)3– 6(y + 2)2 –
– 6(y + 2) – 2 =
= y3 + 6y2 + 12y + 8 – 6y2 –
– 24y – 24 – 6y – 12 – 2 =
= y3 – 18y – 30.
Следовательно, уравнение (13) принимает вид
| y3 – 18y – 30 = 0. | (15) |
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
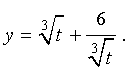 | (16) |
Тогда поскольку
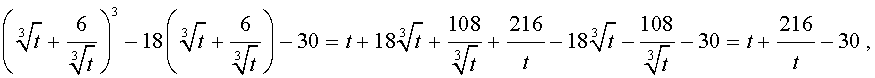
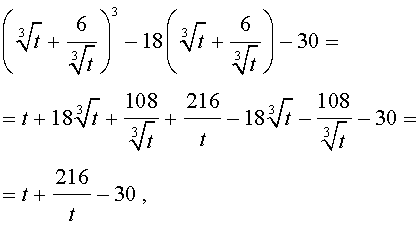
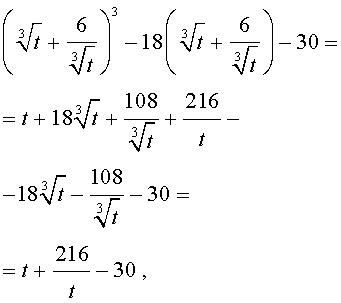
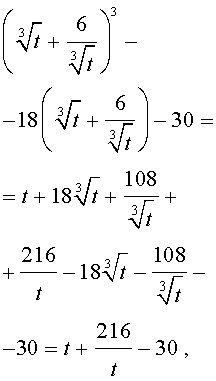
то уравнение (15) примет вид
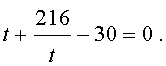 | (17) |
Далее из (17) получаем:
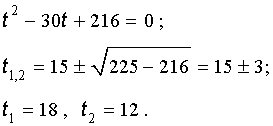
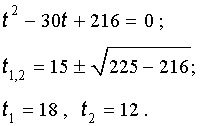
Отсюда по формуле (16) получаем:
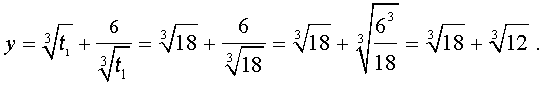 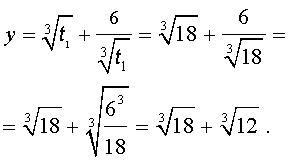 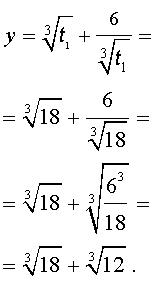 | (18) |
Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
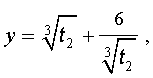
или использовали формулу
![]()
Далее из равенства (18) в соответствии с (14) получаем:
![]()
Таким образом, мы нашли у уравнения (13) вещественный корень
![]()
Замечание 1. У уравнения (13) других вещественных корней нет.
Замечание 2. Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |

