
На этой странице нашего сайта размещены учебные пособия по теории функций комплексного переменного (ТФКП), которые использовались при проведении занятий со студентами МФТИ.
Каждое из учебных пособий содержит теоретические сведения и примеры решения типовых задач по изучаемому разделу теории функций комплексного переменного (ТФКП). Практически все разобранные в учебных пособиях задачи ранее предлагались для решения студентам МФТИ в заданиях для самостоятельной работы, на семестровых контрольных работах и на устных экзаменах по теории функций комплексного переменного (ТФКП). В справочной форме приводится необходимая для решения задач теория.
Мы надеемся, что эти учебные материалы будут полезными не только студентам МФТИ, осваивающим курс теории функций комплексного переменного (ТФКП), но и студентам других ВУЗов.
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Регулярные ветви многозначных функций (часть 1)
В пособии рассматриваются методы решения задач, в которых используются регулярные ветви многозначных функций Ln f(z) и ![]() , где f(z) - голоморфная функция. В качестве примеров приводятся решения задач на разложение регулярных ветвей в ряды Тейлора и Лорана и вычисление интегралов от регулярных ветвей многозначных функций с помощью вычетов.
, где f(z) - голоморфная функция. В качестве примеров приводятся решения задач на разложение регулярных ветвей в ряды Тейлора и Лорана и вычисление интегралов от регулярных ветвей многозначных функций с помощью вычетов.
Содержание
- Регулярные ветви многозначной функции Ln f(z) .
- Регулярные ветви многозначной функции
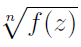 .
. - Примеры решения задач на разложения регулярных ветвей многозначных функций в ряды Тейлора и Лорана
- Примеры решения задач на вычисление интегралов от регулярных ветвей с помощью вычетов.
 Перейти к учебному пособию «Регулярные ветви многозначных функций (часть 1)»
Перейти к учебному пособию «Регулярные ветви многозначных функций (часть 1)»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Регулярные ветви многозначных функций (часть 2)
Это пособие является продолжением пособия «Регулярные ветви многозначных функций (часть 1)» и посвящено методам вычисления интегралов от действительных функций по бесконечному интервалу действительной оси, использующим свойства регулярных ветвей многозначных функций и теорию вычетов.
 Перейти к учебному пособию «Регулярные ветви многозначных функций (часть 2)»
Перейти к учебному пособию «Регулярные ветви многозначных функций (часть 2)»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Регулярные ветви многозначных функций (часть 3)
Пособие является продолжением пособий «Регулярные ветви многозначных функций (часть 1)» и «Регулярные ветви многозначных функций (часть 2)». Пособие посвящено методам вычисления интегралов от действительных функций по конечному интервалу действительной оси, использующим свойства регулярных ветвей многозначных функций и теорию вычетов.
 Перейти к учебному пособию «Регулярные ветви многозначных функций (часть 3)»
Перейти к учебному пособию «Регулярные ветви многозначных функций (часть 3)»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Дистанционное занятие на тему «Принцип аргумента. Теорема Руше»
В пособии рассмотрены методы решения задач, использующие теорему Руше.
Содержание
- Принцип аргумента.
- Теорема Руше.
- Основная терема алгебры.
- Примеры решения задач.
 Перейти к учебному пособию «Принцип аргумента. Теорема Руше»
Перейти к учебному пособию «Принцип аргумента. Теорема Руше»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Принцип максимума модуля голоморфной функции
Пособие посвящено применениям принципа максимума модуля голоморфной функции к решению задач.
 Перейти к учебному пособию «Принцип максимума модуля голоморфной функции»
Перейти к учебному пособию «Принцип максимума модуля голоморфной функции»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Дистанционное занятие на тему «Конформные отображения (часть 1)»
В пособии рассматриваются методы решения задач, в которых требуется построить конформное отображение заданной области расширенной комплексной плоскости на другую заданную область расширенной комплексной плоскости. С этой целью изучаются свойства конформных отображений, в особенности, свойства дробно-линейных отображений.
Содержание
- Определение конформного отображения области расширенной комплексной плоскости на область расширенной комплексной плоскости..
- Свойства конформных отображений.
- Дробно-линейные отображения и их свойства.
- Примеры решения задач.
 Перейти к учебному пособию «Конформные отображения (часть1)»
Перейти к учебному пособию «Конформные отображения (часть1)»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Конформные отображения (часть 2)
Пособие является продолжением пособия «Конформные отображения (часть 1)» и посвящено изучению свойств функции Жуковского, функции, обратной к функции Жуковского, а также комплексной экспоненты.
Содержание
- Функция Жуковского и ее свойства.
- Функция, обратная к функции Жуковского.
- Комплексная экспонента и ее свойства.
- Примеры решения задач.
 Перейти к учебному пособию «Конформные отображения (часть 2)»
Перейти к учебному пособию «Конформные отображения (часть 2)»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Конформные отображения (часть 3)
Пособие является продолжением пособий «Конформные отображения (часть 1)» и «Конформные отображения (часть 2)» и посвящено применениям принципа симметрии и теоремы Римана.
Содержание
- Принцип симметрии.
- Теорема Римана.
- Примеры решения задач.
 Перейти к учебному пособию «Конформные отображения (часть 3)»
Перейти к учебному пособию «Конформные отображения (часть 3)»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Применение методов ТФКП при решении задачи Дирихле для уравнения Лапласа на плоскости
Пособие посвящено применению функций комплексного переменного при решении задачи Дирихле для уравнения Лапласа на плоскости.
Содержание
- Гармонические функции комплексного переменного.
- Инвариантность уравнения Лапласа относительно конформных отображений.
- Постановка задачи Дирихле для уравнения Лапласа на плоскости.
- Формула Пуассона для решения задачи Дирихле в круге.
- Примеры решения задач.
