Справочник по математике Геометрия (Стереометрия)
Геометрия (Стереометрия) Призмы
Призмы
Призмы
Содержание
 |
Основные определения и свойства призм. Теорема Эйлера |
 |
Виды призм. Прямые и наклонные призмы. Правильные призмы |
 |
Примеры призм. Треугольные призмы. Четырехугольные призмы. Параллелепипеды |

Основные определения и свойства призм. Теорема Эйлера
ОПРЕДЕЛЕНИЯ
 |
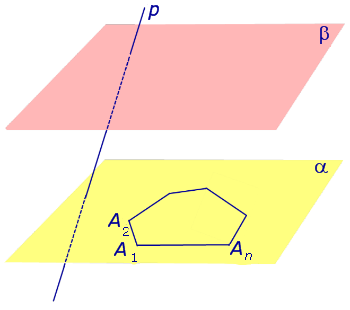
Рассмотрим две параллельные плоскости α и β , прямую p , пересекающую эти плоскости, и произвольный выпуклый n – угольник A1A2 ... An , лежащий в плоскости α (рис. 1).
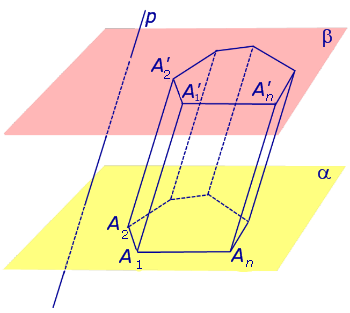
Рис.1 Если через каждую точку многоугольника A1A2 ... An провести прямую, параллельную прямой p , и обозначить символами A'1, A'2, ... , A'n точки пересечения с плоскостью β прямых, параллельных прямой p и проходящих через точки A1, A2, ... , An , то полученную фигуру A1A2 ... An A'1A'2 ... A'n называют n – угольной призмой (рис.2).
Рис.2 |
 |
A1A2A'2A'1, A2A3A'3A'2, ... , AnA1A'1A'n называют боковыми гранями призмы. |
 |
Совокупность всех боковых граней призмы составляет боковую поверхность призмы. |
 |
Многоугольники A1A2 ... An и A'1A'2 ... A'n называют основаниями призмы. |
 |
Точки A1, A2, ... , An , A'1, A'2, ... , A'n (вершины многоугольников A1A2 ... An и A'1A'2 ... A'n ) называют вершинами призмы. |
 |
Отрезки A1A'1 , A2A'2 , ... , AnA'n называют боковыми ребрами призмы. |
 |
Отрезки A1A2 , A2A3 , ... , AnA1 , ... , A'1A'2 , A'2A'3 , ... , A'nA'1 (стороны многоугольников A1A2 ... An и A'1A'2 ... A'n ) называют ребрами оснований призмы. |
 |
Расстояние между плоскостями, на которых лежат основания призмы, называют высотой призмы. |
 |
Диагональю призмы называют отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. |
ЗАМЕЧАНИЕ 1. В случае, когда не требуется делать специальных уточнений,
 |
боковые ребра и ребра оснований называют ребрами призмы, |
 |
боковые грани и основания призмы называют гранями призмы |
 |
совокупность всех граней призмы (всех боковых граней и оснований) называют полной поверхностью призмы, |
 |
n – угольные призмы называют призмами. |
УТВЕРЖДЕНИЕ 1. Каждая из n боковых граней призмы
A1A2A'2A'1, A2A3A'3A'2, ... , AnA1A'1A'n
является параллелограммом.
ДОКАЗАТЕЛЬСТВО. Докажем сначала, что параллелограммом является, например, четырехугольник A1A2A'2A'1. Для этого заметим, что стороны A1A'1 и A2A'2 параллельны по построению. Заметим также, что прямая A1A2 параллельна плоскости β , так как лежит в плоскости α , которая параллельна плоскости β . Прямая A'1A'2 является линией пересечения плоскости A1A2A'2A'1 с плоскостью β . Из признака параллельности прямой и плоскости следует, что прямая A'1A'2 параллельна прямой A1A2 . Таким образом, у четырехугольника A1A2A'2A'1 противоположные стороны попарно параллельны, то есть A1A2A'2A'1 – параллелограмм.
Для остальных четырехугольников доказательство проводится аналогично.
УТВЕРЖДЕНИЕ 2 . Все боковые ребра призмы равны.
Это утверждение непосредственно вытекает из утверждения 1.
ТЕОРЕМА ЭЙЛЕРА . Для любой призмы справедливо равенство:
|
+ |
|
– |
|
= | 2 |
ДОКАЗАТЕЛЬСТВО. Заметим, что у n – угольной призмы 2n вершин, n боковых граней, 2 основания, 2n ребер основания и n боковых ребер. Следовательно, у n – угольной призмы (n + 2) грани и 3n ребер.
Поскольку
2n + (n + 2) – 3n = 2
то теорема Эйлера доказана.
Виды призм. Прямые и наклонные призмы. Правильные призмы
Существует следующая классификация призм.
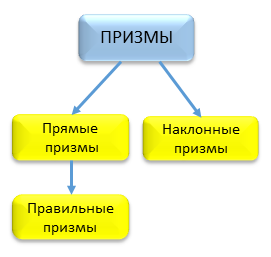
Рис.3
ОПРЕДЕЛЕНИЯ
 |
Прямой призмой называют призму, боковые ребра которой перпендикулярны к плоскостям оснований. |
 |
Призмы, боковые ребра которых не перпендикулярны к плоскостям оснований, называют наклонными призмами. |
 |
Правильной призмой называют прямую призму, основаниями которой служат правильные многоугольники. |
ЗАМЕЧАНИЕ 2. Все боковые грани прямой призмы являются прямоугольниками. Высота прямой призмы равна длине бокового ребра.
Примеры призм. Треугольные призмы. Четырехугольные призмы.
Параллелепипеды
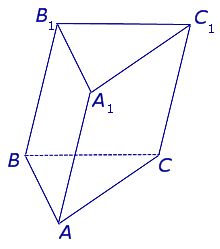
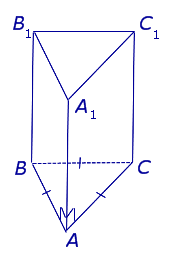
| Наклонная треугольная призма |
|
Свойства:
|
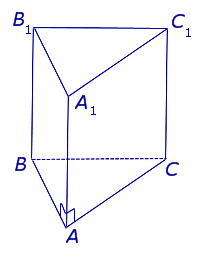
| Прямая треугольная призма |
|
Свойства:
|
| Правильная треугольная призма |
|
Свойства:
|
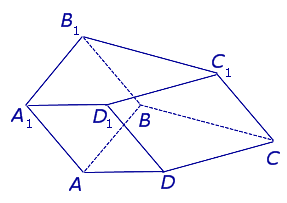
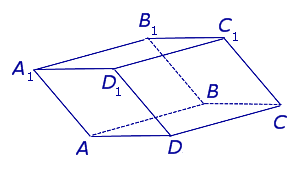
| Наклонная четырехугольная призма |
|
Свойства:
|
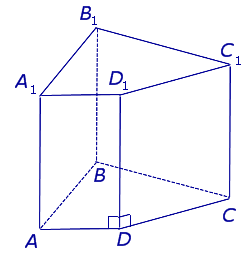
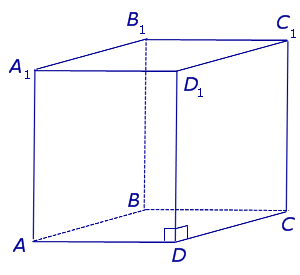
| Прямая четырехугольная призма |
|
Свойства:
|
| Правильная четырехугольная призма |
|
Свойства:
|
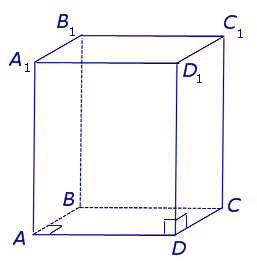
| Параллелепипед |
|
Свойства:
|
| Прямой параллелепипед |
|
Свойства:
|
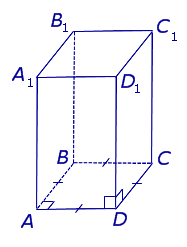
| Прямоугольный параллелепипед |
|
Свойства:
|
| Правильный параллелепипед |
|
Свойства:
|
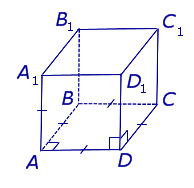
| Куб |
|
Свойства: |
Близкие по тематике разделы сайта
С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».
С определением сечения призмы и способами построения сечений призмы можно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».