Справочник по математике Геометрия (Стереометрия)
Геометрия (Стереометрия) Призмы
Призмы
Сечения призмы. Перпендикулярные сечения призмы
Содержание
 |
Сечения призмы |
 |
Перпендикулярные сечения призмы |

Сечения призмы
ОПРЕДЕЛЕНИЕ 1. Сечением тела некоторой плоскостью α называют фигуру, состоящую из всех точек этого тела, лежащих в плоскости α.
В качестве примера рассмотрим сечение куба ABCDA1B1C1D1 плоскостью, проходящей через точку D и середины ребер A1B1 и B1C1 . Рассмотрим процесс построения сечения подробно.
Обозначим буквами E и F середины ребер A1B1 и B1C1 (рис. 1).
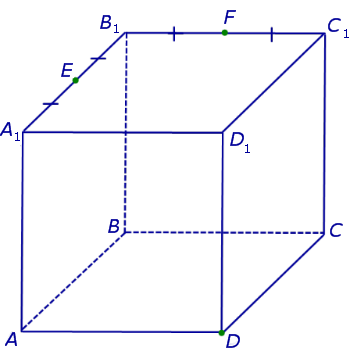
Рис.1
Поскольку точки E и F лежат на ребрах одной грани куба A1B1C1D1 , то проведем прямую EF до пересечения с продолжениями двух других ребер этой грани. Обозначим буквой G точку пересечения прямой EF с продолжением отрезка D1C1 за точку C1, а буквой Н – точку пересечения прямой EF с продолжением отрезка D1A1 за точку A1 . Эти точки пересечения существуют, поскольку все указанные прямые лежат в одной плоскости A1B1C1D1 и не параллельны попарно (рис. 2).
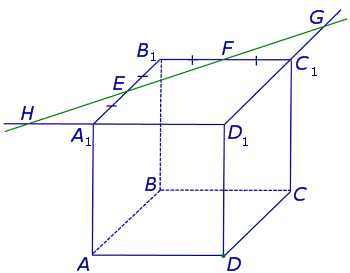
Рис.2
Точки G и D принадлежат плоскости сечения, а, значит, и вся прямая DG лежит в плоскости сечения. С другой стороны, эти точки лежат на ребрах (или их продолжениях) одной грани куба DD1C1C. Значит, точка пересечения DG с ребром куба C1C (точка N ) будет принадлежать сечению. Таким образом, мы получаем еще два отрезка сечения: FN и DN (рис. 3).
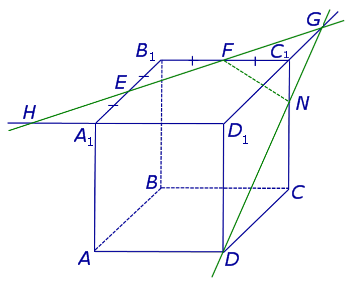
Рис.3
Теперь, действуя аналогичным образом, проводим прямую HD, обозначаем точку пересечения этой прямой с ребром AA1 буквой M и проводим линии сечения ME и MD в плоскостях граней AA1B1B и AA1D1D (рис. 4).
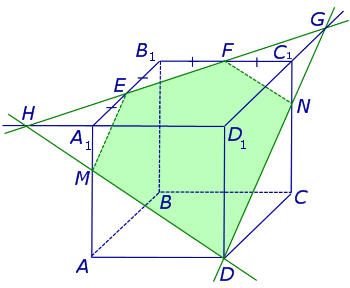
Рис.4
В результате, как и показано на рисунке 4, получаем, что искомое сечение – пятиугольник DMEFN.
Предлагаем посетителю нашего сайта решить в качестве полезного упражнения следующую задачу.
ЗАДАЧА. Найти площадь сечения DMEFN, если ребро куба равно 6.
УКАЗАНИЕ К РЕШЕНИЮ. Треугольники HA1E, EB1F и FC1G равны.
Перпендикулярные сечения призмы
ОПРЕДЕЛЕНИЕ 2. Перпендикулярным сечением призмы называют такое сечение, плоскость которого пересекает все боковые ребра призмы и перпендикулярна к ним.
На рисунке 5 построено перпендикулярное сечение наклонной треугольной призмы – треугольник KLM. Хотим обратить Ваше внимание на то, что призма на рисунке 5 изображена лежащей на одной из своих боковых граней. Такой способ представления призмы на чертеже часто очень удобен при решении задач.
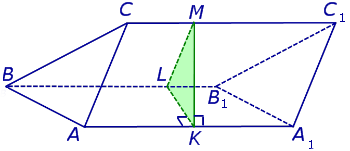
Рис.5
ЗАМЕЧАНИЕ. Все перпендикулярные сечения призмы равны между собой.
Близкие по тематике разделы сайта
С понятием призмы и различными видами призм можно ознакомиться в разделе «Призмы».
С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».
