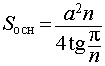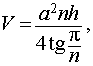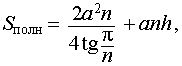Справочник по математике Геометрия (Стереометрия)
Геометрия (Стереометрия) Призмы
Призмы
Формулы для объема, площади боковой поверхности и площади полной поверхности призмы
Введем следующие обозначения:
| V | объем призмы |
| Sбок | площадь боковой поверхности призмы |
| Sполн | площадь полной поверхности призмы |
| Sосн | площадь основания призмы |
| Pосн | периметр основания призмы |
| Pперп | периметр перпендикулярного сечения призмы |
| Sперп | площадь перпендикулярного сечения призмы |
Используя эти обозначения, составим таблицу с формулами для вычисления объемов, площадей боковой поверхности и площадей полной поверхности различных видов призм.
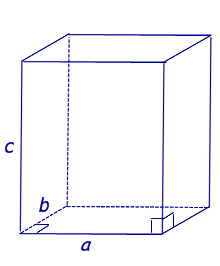
| Куб |
|
Формулы для объема, площади боковой и полной поверхности: V = a3, Sбок = 4a2, Sполн = 6a2, где a – длина ребра куба. |
| Прямоугольный параллелепипед |
|
Формулы для объема, площади боковой и полной поверхности: V = abc, Sбок = 2ac + 2bc, Sполн = 2ac + 2bc +2ab, где |
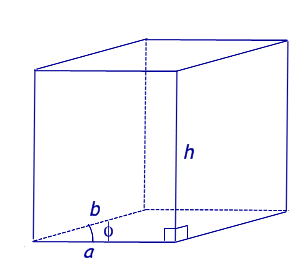
| Прямой параллелепипед, в основании которого лежит параллелограмм со сторонами a, b и углом φ |
|
Формулы для объема, площади боковой и полной поверхности: Sосн = ab sin φ, V = Sосн h = abh sin φ, Sбок = 2ah + 2bh, Sполн = 2ab sin φ + 2ah + 2bh, где |
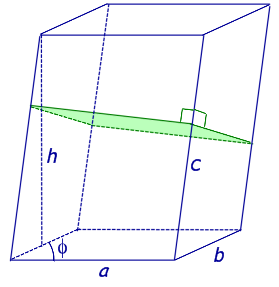
| Произвольный параллелепипед |
|
Формулы для объема, площади боковой и полной поверхности: Sосн = ab sin φ, V = Sосн h = abh sin φ, V = Sперп с, Sбок = Pперп с, Sполн = 2ab sin φ + Pперп с, где |
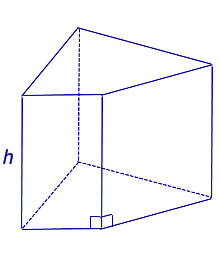
| Прямая призма |
|
Формулы для объема, площади боковой и полной поверхности: V = Sосн h, Sбок = Pосн h, Sполн = 2Sосн + Sбок, где |
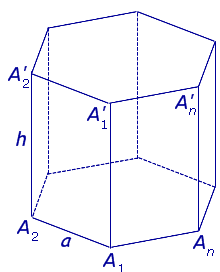
| Правильная n – угольная призма |
|
Формулы для объема, площади боковой и полной поверхности:
(см. раздел «правильные многоугольники»), V = Sосн h,
Sбок = Pосн h = anh, Sполн = 2Sосн + Sбок,
где |
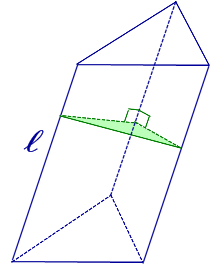
| Произвольная призма |
|
Формулы для объема, площади боковой и полной поверхности: V = Sосн h, V = Sперп l, Sбок = Pперп l, Sполн = 2Sосн + Sбок, где |
Близкие по тематике разделы сайта
С понятием призмы и различными видами призм можно ознакомиться в разделе «Призмы».
С определением сечения призмы и способами построения сечений призмы можно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».