Справочник по математике Тригонометрия
Тригонометрия
Тригонометрические функции острого угла
Катеты BC и AC прямоугольного треугольника ABC (рис. 1) называют противолежащим катетом угла α и прилежащим катетом угла α соответственно.

Рис.1
Катеты AC и BC прямоугольного треугольника ABC (рис. 2) называют противолежащим катетом угла β и прилежащим катетом угла β соответственно.
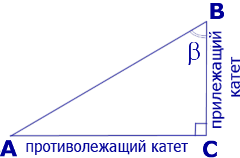
Рис.2
Синусом угла называют дробь:
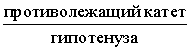
Косинусом угла называют дробь:
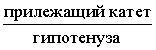
Тангенсом угла называют дробь:
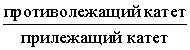
Котангенсом угла называют дробь:
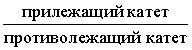
Синус, косинус, тангенс и котангенс, и их комбинации называют тригонометрическими функциями. В данном разделе справочника тригонометрические функции вводятся для острых углов. В следующем разделе даётся определение тригонометрических функций для произвольных углов.
Для синуса, косинуса, тангенса и котангенса угла α используют обозначения
sin α , cos α , tg α , ctg α
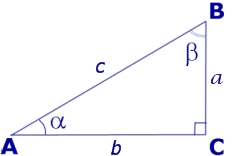
Рис.3
В соответствии с рисунком 3 справедливы формулы:
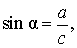
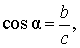
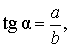
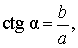
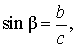
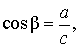
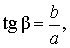
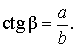
Следовательно,
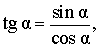
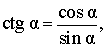
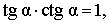
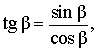
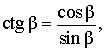
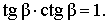
Кроме того, справедливы формулы:
sin α = cos β, cos α = sin β, tg α = ctg β, ctg α = tg β,
которые можно переписать в виде:
sin α = cos (90° – α), cos α = sin (90° – α),
tg α = ctg (90° – α), ctg α = tg (90° – α).
ПРИМЕР. Найти тригонометрические функции углов 30°, 45°, 60°.
РЕШЕНИЕ. Рассмотрим равносторонний треугольник ABC, сторона которого равна 2 (рис. 4), и проведем высоту BD.
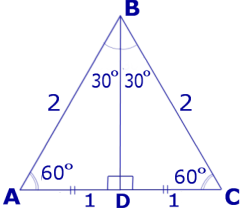
Рис.4
Тогда
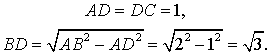
Поэтому
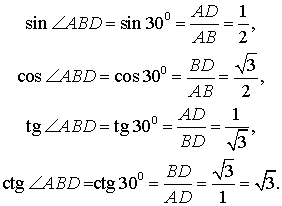
Кроме того
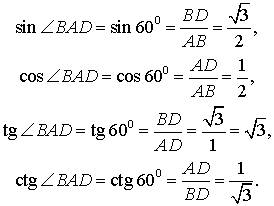
Теперь рассмотрим прямоугольный равнобедренный треугольник ABC, катеты которого равны 1 (рис. 5).
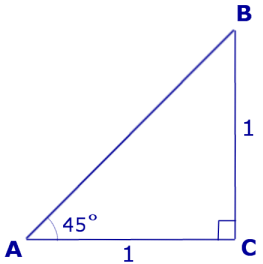
Тогда
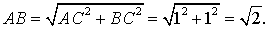
Поэтому
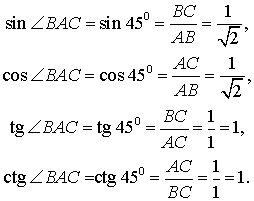
Определение тригонометрических функций произвольного угла приводится в разделе справочника "Тригонометрические функции произвольного угла".
