Справочник по математике Тригонометрия
Тригонометрия
Формулы приведения
Содержание
 |
Таблица формул приведения |

Рассмотрим рисунок 1.
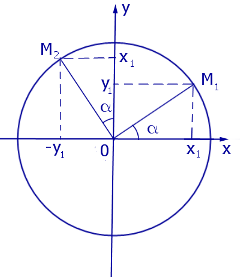
Рис.1
На этом рисунке
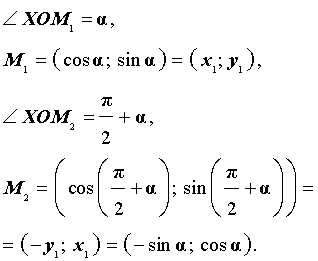
Следовательно, справедливы формулы:
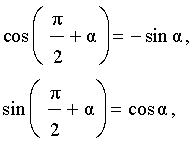 |
(1) |
откуда вытекают формулы:
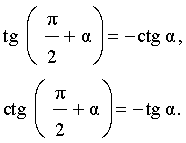 |
(2) |
Если же в формулах (1) и (2) сделать замену: α → – α, то, воспользовавшись свойствами четности тригонометрических функций, мы получим формулы:
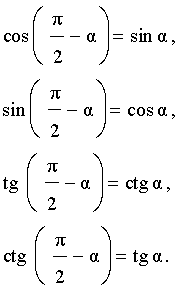 |
(3) |
Формулы (1), (2), (3) называют формулами приведения.
Таблица формул приведения
В целом формулы приведения удобно представить в виде следующей таблицы.
ТАБЛИЦА - Формулы приведения
| sin (– α) = – sin α; |
| cos (– α) = cos α; |
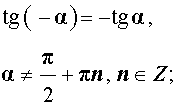 |
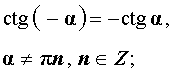 |
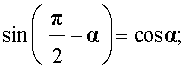 |
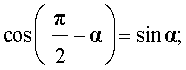 |
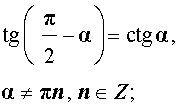 |
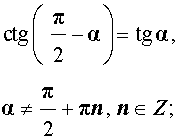 |
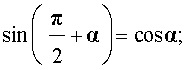 |
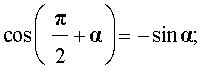 |
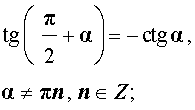 |
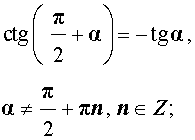 |
| sin (π – α) = sin α; |
| cos (π – α) = – cos α; |
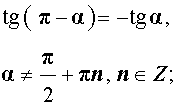 |
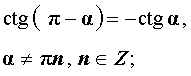 |
| sin (π + α) = – sin α |
| cos (π + α) = – cos α |
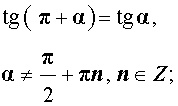 |
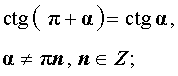 |
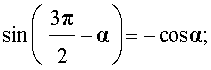 |
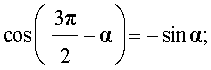 |
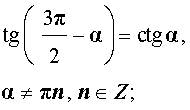 |
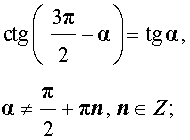 |
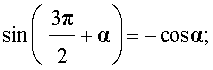 |
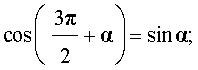 |
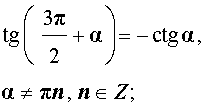 |
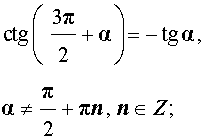 |
| sin (2π – α) = – sin α |
| cos (2π – α) = cos α |
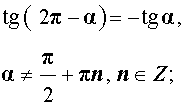 |
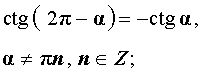 |
| sin (2π + α) = sin α |
| cos (2π + α) = cos α |
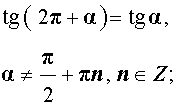 |
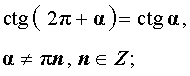 |
