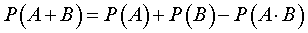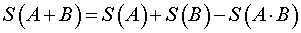Справочник по математике Теория вероятностей и статистика
Теория вероятностей и статистика Теория вероятностей
Теория вероятностей
Вероятность суммы двух событий. Независимость двух событий. Вероятность произведения двух независимых событий
Содержание
 |
Вероятность суммы двух событий |
 |
Несовместные события |
 |
Независимость двух событий. Вероятность произведения двух независимых событий |

Вероятность суммы двух событий
Пусть A и B – два произвольных события в случайном эксперименте с множеством элементарных исходов Ω .
Справедливо следующее утверждение.
УТВЕРЖДЕНИЕ 1. Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения.
Другими словами, верна формула:
|
|
(1) |
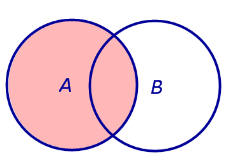
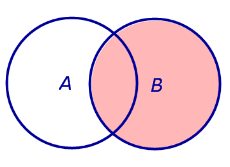
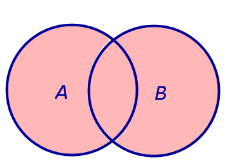
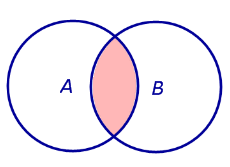
ДОКАЗАТЕЛЬСТВО. Рассмотрим диаграммы Эйлера – Венна для суммы двух событий и произведения двух событий, разместив их на одном рисунке (рис.1).
|
||||||||
|
Рис.1 |
Проведем доказательство утверждения 1 на примере геометрического определения вероятности.
Если площадь произвольной фигуры F обозначить символом S (F) , то из рисунка 1 легко установить справедливость равенства:
|
|
(2) |
которое словами можно выразить так: «Площадь фигуры A + B равна сумме площадей фигур A и B минус площадь фигуры 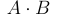 ».
».
Если обе части равенства (2) разделить на число S (Ω) , то мы получим равенство
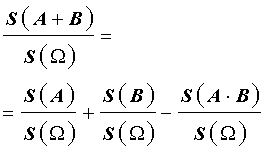 |
(3) |
В силу геометрического определения вероятности справедливы формулы
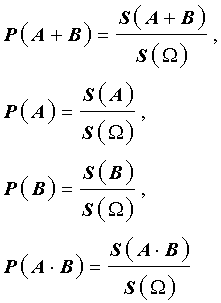
с помощью которых равенство (3) преобразуется к виду (1), что и завершает доказательство утверждения 1.
Доказательство утверждения 1 для классического определения вероятности проводится аналогичным образом, и мы оставляем его читателю в качестве полезного упражнения.
Несовместные события
ОПРЕДЕЛЕНИЕ. Два события A и B называют несовместными, если они не пересекаются.
Другими словами, события A и B несовместны, если
![]()
ЗАМЕЧАНИЕ 1. События A и B несовместны в том, и только в том случае, если событие B является подмножеством события 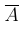 , то есть
, то есть 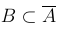 .
.
ЗАМЕЧАНИЕ 2. События A и B несовместны в том, и только в том случае, если событие A является подмножеством события 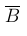 , то есть
, то есть 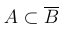 .
.
ЗАМЕЧАНИЕ 3. Если события A и B несовместны, то вероятность их произведения равна нулю.
Другими словами, для несовместных событий A и B верна формула
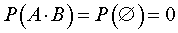
ЗАМЕЧАНИЕ 4. Если события A и B несовместны, то вероятность суммы событий A + B равна сумме вероятностей событий A и B .
Другими словами, для несовместных событий A и B верна формула
P (A + B) = P (A) + P (B)
Независимость двух событий. Вероятность произведения двух независимых событий
Два события A и B называют независимыми, если появление одного из этих событий никак не влияет на вероятность появления второго события.
ЗАМЕЧАНИЕ 5. Несовместные события и независимые события – это совершенно разные понятия, и их не следует путать.
Справедливо следующее утверждение.
УТВЕРЖДЕНИЕ 2. Вероятность произведения двух независимых событий равна произведению их вероятностей.
Другими словами, для двух независимых событий A и B верна формула
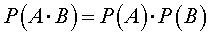 |
(4) |
Проиллюстрируем справедливость формулы (4) на примере.
ПРИМЕР 1. Случайный эксперимент состоит в подбрасывании двух игральных костей. Одна из игральных костей окрашена в синий цвет, другая – в красный. Найти вероятность того, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 .
РЕШЕНИЕ. Сформируем следующую таблицу, в которой записаны все 36 возможных вариантов пар чисел, выпадающих при подбрасывании двух игральных костей. Первая строка таблицы – это числа, выпавшие при бросании синей кости, а первый столбец таблицы – это числа, выпавшие при бросании красной кости. На пересечении строки и столбца указана пара чисел, выпавших на двух костях.
 |
1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 1, 5 | 1, 6 |
| 2 | 2, 1 | 2, 2 | 2, 3 | 2, 4 | 2, 5 | 2, 6 |
| 3 | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 3, 5 | 3, 6 |
| 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 | 4, 5 | 4, 6 |
| 5 | 5, 1 | 5, 2 | 5, 3 | 5, 4 | 5, 5 | 5, 6 |
| 6 | 6, 1 | 6, 2 | 6, 3 | 6, 4 | 6, 5 | 6, 6 |
Благоприятным является только один исход, а именно, клетка с результатом 4, 3 , окрашенная в таблице желтым цветом. Следовательно, вероятность события, состоящего в том, что на синей игральной кости выпадает число 3 , а на красной игральной кости выпадает число 4 , равна 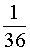 .
.
Теперь рассмотрим случайный эксперимент, описанный в примере 1, с другой стороны. Для этого обозначим буквой A случайное событие, состоящее в том, что на синей игральной кости выпадает число 3 , а буквой B - случайное событие, состоящее в том, что на красной игральной кости выпадает число 4 . События A и B являются независимыми событиями, а их вероятности равны:
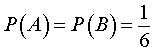
Событие 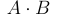 состоит в том, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 . Поскольку,
состоит в том, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 . Поскольку,
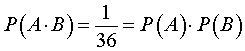
то в рассматриваемом случайном эксперименте по подбрасыванию двух игральных костей формула (4) верна.
В заключение приведем ещё одну иллюстрацию применимости формулы для вероятности суммы двух событий и формулы для вероятности произведения двух независимых событий.
ПРИМЕР 2. Два стрелка стреляют по мишени. Первый стрелок поражает мишень с вероятностью 0,9 . Второй стрелок поражает мишень с вероятностью 0,8 . Найти вероятность того, что мишень будет поражена.
РЕШЕНИЕ. Обозначим буквой A случайное событие, состоящее в том, что в мишень попадает первый стрелок, а буквой B обозначим случайное событие, состоящее в том, что в мишень попадает второй стрелок. Тогда событие A + B означает, что мишень поражена, а событие 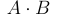 означает, что в мишень попали оба стрелка. По условию
означает, что в мишень попали оба стрелка. По условию
P (A) = 0,9 и P (B) = 0,8
а поскольку события A и B независимы, то в силу формулы (4)
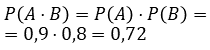
Воспользовавшись формулой (1), находим
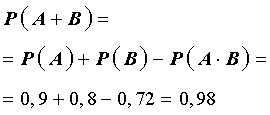
ОТВЕТ: 0,98