Справочник по математике Теория вероятностей и статистика
Теория вероятностей и статистика Теория вероятностей
Теория вероятностей
Геометрическое определение вероятности
Как было показано в разделе «Классическое определение вероятности», в случайных экспериментах с конечным числом равновозможных элементарных исходов применяется классическое определение вероятности.
Для введения вероятности событий в случайных экспериментах, возможные результаты которых (элементарные исходы) также являются равновозможными и целиком заполняют отрезок прямой линии, фигуру на плоскости или область в пространстве, применяется геометрическое определение вероятности. В таких экспериментах число элементарных исходов не является конечным, и поэтому классическое определение вероятности к ним применять нельзя.
Проиллюстрируем введение геометрического определения вероятности на примерах.
ПРИМЕР 1. На отрезок числовой прямой [2, 16] наугад брошена точка. Найти вероятность того, что точка попала на отрезок [5, 9] (рис.1).
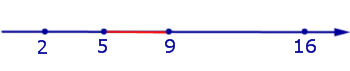
Рис.1
РЕШЕНИЕ. Множеством элементарных исходов случайного эксперимента по бросанию точки служит множество всех точек отрезка [2, 16], то есть
Ω = [2, 16] .
Попадание точки на отрезок [5, 9] является одним из случайных событий, которое мы обозначим буквой A :
A = [5, 9] .
При геометрическом определении вероятность события A вычисляется по формуле
 |
(1) |
Поскольку длина отрезка [5, 9] равна 4, а длина отрезка [2, 16] равна 14, то в соответствии с формулой (1) находим
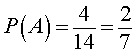
ОТВЕТ: 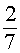
ПРИМЕР 2. Диагонали KM и LN квадрата KLMN пересекают вписанную в квадрат окружность в точках E и F , точка O – центр окружности (рис. 2).
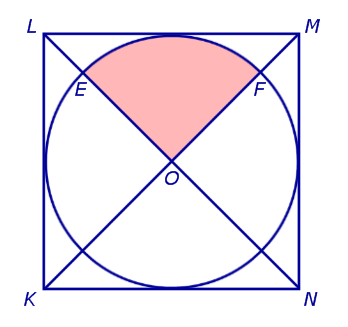
Рис.2
В квадрат KLMN наугад брошена точка. Найти вероятность того, что точка попадет в сектор EOF, отмеченный на рисунке 2 розовым цветом.
РЕШЕНИЕ. Множеством элементарных исходов Ω случайного эксперимента по бросанию точки служит множество всех точек квадрата KLMN .
Попадание точки в круговой сектор EOF является одним из случайных событий, которое мы обозначим буквой A .
При геометрическом определении вероятность события A вычисляется по формуле
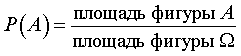 |
(2) |
Если обозначить буквой R радиус вписанного в квадрат KLMN круга, то площадь сектора EOF будет равна
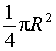 ,
,
сторона квадрата KLMN будет равна 2R , а площадь квадрата KLMN будет равна 4R2 .
Поскольку в этом случае площадь фигуры A равна
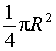 ,
,
а площадь фигуры Ω равна 4R2 , то в соответствии с формулой (2) находим
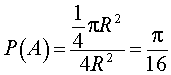
ОТВЕТ: 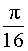
ПРИМЕР 3. В конус с вершиной S и центром основания O наугад брошена точка. Найти вероятность того, что точка попадет в усеченный конус, полученный при сечении конуса плоскостью, проходящей через середину O' высоты конуса и параллельной основанию конуса (рис. 3).
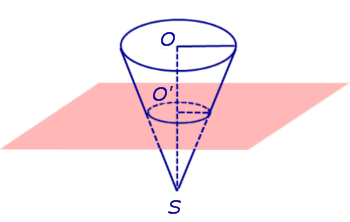
Рис.3
РЕШЕНИЕ. Множеством элементарных исходов Ω случайного эксперимента по бросанию точки служит множество всех точек конуса с вершиной S и центром основания O .
Попадание точки в усеченный конус является одним из случайных событий, которое мы обозначим буквой A .
При геометрическом определении вероятность события A вычисляется по формуле
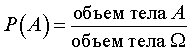 |
(3) |
Обозначим буквой R радиус основания конуса с вершиной S и центром основания O , а буквой H – высоту этого конуса. Тогда радиус основания и высота конуса с вершиной S и центром основания O' будут равны
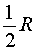 и
и 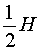
соответственно.
Объем конуса с вершиной S и центром основания O равен
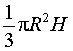 ,
,
конуса с вершиной S и центром основания O1 равен
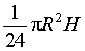 .
.
Поэтому объем усеченного конуса равен
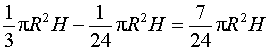 .
.
Поскольку в этом случае объем тела A равен
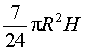 ,
,
а объем тела Ω равен
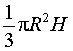 ,
,
то, воспользовавшись формулой (3), получаем
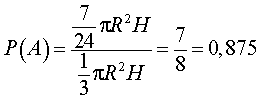
ОТВЕТ: 0,875 .
ЗАМЕЧАНИЕ. Применение формул (1), (2) и (3) для определения вероятности событий в случайных экспериментах, элементарные исходы которых целиком заполняют отрезок прямой линии, фигуру на плоскости или область в пространстве, соответственно, и составляет суть введения геометрического определения вероятности.
