Справочник по математике
Элементы математического анализа Производная функции
Исследование функции на выпуклость вверх и выпуклость вниз с помощью второй производной
Содержание
Выпуклые вверх функции
ОПРЕДЕЛЕНИЕ 1. Функцию y = f (x) называют выпуклой вверх на интервале (a, b), если для любых двух точек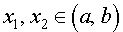 
таких, что x1 < x2 , график функции y = f (x) расположен выше отрезка, соединяющего точки A1 = (x1; f (x1)) и A2 = (x2; f (x2)) .
Функция, график которой изображен на рисунке 1, выпукла вверх на интервале (a, b) .
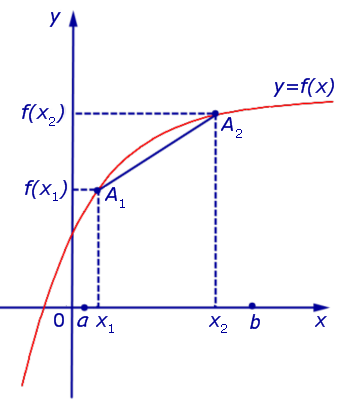
Рис.1
ПРИМЕР 1. Примером функции, выпуклой вверх на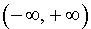 
, является функция y = – x2 (рис. 2).
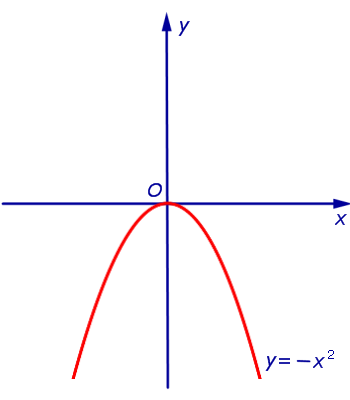
Рис.2
Выпуклые вниз функции
ОПРЕДЕЛЕНИЕ 2. Функцию y = f (x) называют выпуклой вниз на интервале (a, b), если для любых двух точек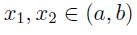 
таких, что x1 < x2 , график функции y = f (x) расположен ниже отрезка, соединяющего точки A1 = (x1; f (x1)) и A2 = (x2; f (x2)) .
Функция, график которой изображен на рисунке 3, выпукла вниз на интервале (a, b) .
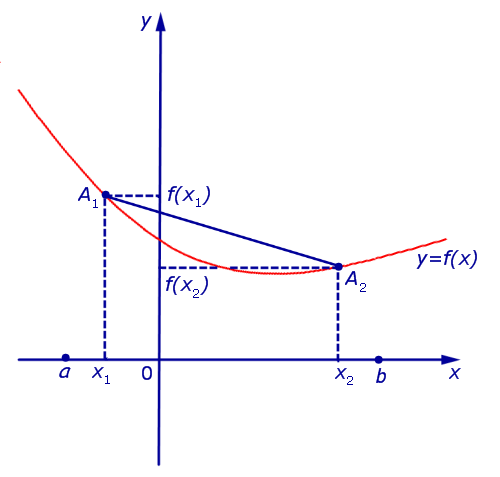
Рис.3
ПРИМЕР 2. Примером функции, выпуклой вниз на 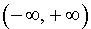, является функция y = x2 (рис. 4).
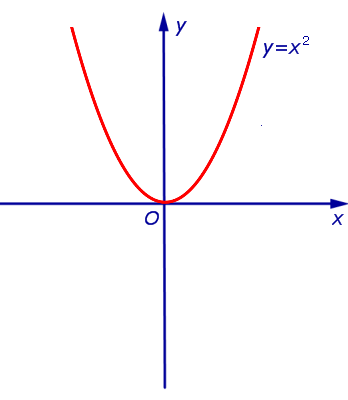
Рис.4
Вторая производная функции
ОПРЕДЕЛЕНИЕ 3. Если у функции y = f (x) существует производная в некоторой точке x0 , то эту производную часто называют первой производной или производной первого порядка функции y = f (x) в точке x0 .
Пусть у функции y = f (x) существует производная во всех точках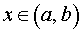 
. Тогда, вычисляя в каждой точке 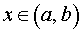производную f ' (x), мы получим функцию y = f ' (x). Если у функции y = f ' (x) существует производная в некоторой точке x0 интервала (a, b), то эту производную называют второй производной или производной второго порядка функции y = f (x) в точке x0 .
Для производной второго порядка y = f (x) используются обозначения:
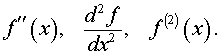
Например,
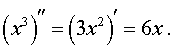
Точно так же, как это было сделано при определении второй производной функции f (x), можно определить и производные более высоких порядков: третью производную, четвертую производную и т.д. (конечно же, при условии, что они существуют).
Достаточные условия выпуклости вверх и выпуклости вниз функции
При исследовании направления выпуклости функции (выпуклость вверх или выпуклость вниз) важную роль играет вторая производная этой функции.
УТВЕРЖДЕНИЕ 1. Если функция f (x) имеет на интервале (a, b) вторую производную, причем для всех 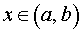выполнено условие
f '' (x) > 0 ,
то функция f (x) выпукла вниз на интервале (a, b).
УТВЕРЖДНИЕ 2. Если функция f (x) имеет на интервале (a, b) вторую производную, причем для всех 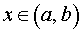выполнено условие
f '' (x) < 0 ,
то функция f (x) выпукла вверх на интервале (a, b).
Доказательства утверждений 1 и 2 выходят за рамки школьного курса математики и здесь не приводятся.
ПРИМЕР 3. Функция y = ln x на интервале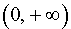 
удовлетворяет условию
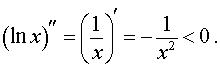
В силу утверждения 2 отсюда следует, что функция y = ln x выпукла вверх (рис. 5) на всей своей области определения .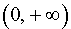
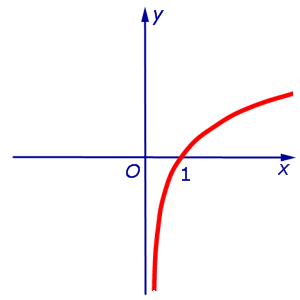
Рис.5
ПРИМЕР 4. Функция y = e x на интервале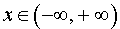 
удовлетворяет условию
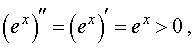
и, в силу утверждения 1, функция y = e x выпукла вниз (рис. 6) на всей своей области определения .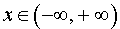
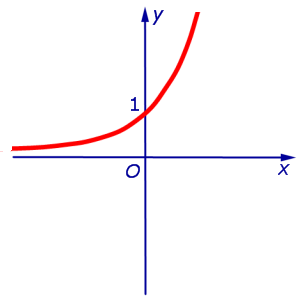
Рис.6
Точки перегиба
ОПРЕДЕЛЕНИЕ 4. Пусть функция y = f (x) определена на некотором интервале (a, b) , содержащем точку x0 . Говорят, что при переходе через точку x0 функция f (x) меняет направление выпуклости, если на одном из интервалов
(a, x0) и (x0, b)
функция выпукла вверх, а на другом – выпукла вниз.
ОПРЕДЕЛЕНИЕ 5. Пусть функция y = f (x) определена на некотором интервале (a, b) , содержащем точку x0 , а у графика функции в точке (x0; f (x0)) существует касательная. Если функция f (x) при переходе через точку x0 меняет направление выпуклости, то точку x0 называют точкой перегиба функции f (x) .
ЗАМЕЧАНИЕ 1 . Если x0 – точка перегиба функции y = f (x), то график функции y = f (x) при переходе через точку x0 переходит с одной стороны от касательной в точке (x0; f (x0)) на другую сторону от касательной, то есть «перегибается» через касательную.
ПРИМЕР 5. Рассмотрим функцию y = x3, график которой изображен на рисунке 7.
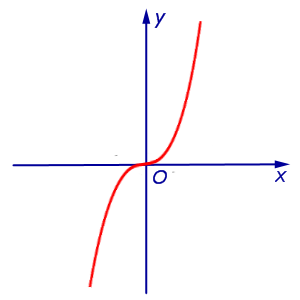
Рис.7
Поскольку
y (0) = 0, y' (0) = 0,
то прямая y = 0 (ось абсцисс Ox ) является касательной к графику функции y = x3 в точке (0; 0).
Кроме того,
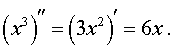
Поэтому y" > 0 при x > 0 и y" < 0 при x < 0 . Таким образом, функция y = x3 выпукла вверх при x < 0 и выпукла вниз при x > 0 , и точка x = 0 является точкой перегиба графика функции y = x3. График функции y = x3 при переходе через точку (0; 0) переходит из нижней полуплоскости в верхнюю полуплоскость, то есть «перегибается» через касательную y = 0 .
Необходимые условия для существования точки перегиба
УТВЕРЖДЕНИЕ 3. Если точка x0 является точкой перегиба графика функции f (x), то в точке x0 либо вторая производная f '' (x) = 0 , либо f '' (x) не существует.
ЗАМЕЧАНИЕ 2. Условия существования точки перегиба, сформулированные в утверждении 3, являются необходимыми, но не являются достаточными.
Действительно, рассмотрим функцию y = x4, график которой изображен на рисунке 8.
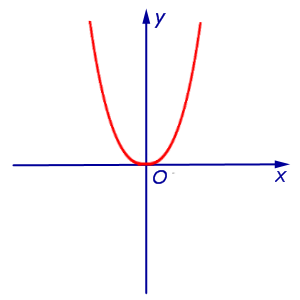
Рис.8
Вычисляя вторую производную этой функции
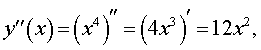
замечаем, что y '' (0) = 0 , однако точка x = 0 не является точкой перегиба графика функции y = x4, так как функция y = x4 выпукла вниз, как при x < 0 , так и при x > 0 .
Достаточные условия для существования точки перегиба
УТВЕРЖДЕНИЕ 4. Пусть функция y = f (x) определена на некотором интервале (a, b) , содержащем точку x0 , имеет первую производную в каждой точке интервала (a, b) и имеет вторую производную в каждой точке интервала (a, b) за исключением, быть может, самой точки x0 .
Если для точек 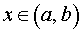выполнено условие:
f '' (x) > 0 при x < x0 и f '' (x) < 0 при x > x0 ,
либо выполнено условие:
f '' (x) < 0 при x < x0 и f '' (x) > 0 при x > x0 ,
то точка x0 является точкой перегиба графика функции f (x).
Другими словами, точка x0 является точкой перегиба графика функции f (x), если при переходе через точку x0 вторая производная функции меняет свой знак.
ПРИМЕР 6. Найти интервалы, на которых функция
y (x) = x4 – 6x3 + 12x2
выпукла вверх, а также интервалы, на которых эта функция выпукла вниз. Определить точки перегиба.
РЕШЕНИЕ. Вычислим вторую производную функции:
y' (x) = 4x3 – 18x2 + 24x ,
y'' (x) = 12x2 – 36x + 24 =
=12(x2 – 3x + 2) = 12(x – 1) (x – 2) .
Отсюда вытекает, что вторая производная существует во всех точках 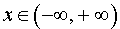и обращается в нуль в точках x = 1 и x = 2 . Воспользуемся методом интервалов и изобразим на рисунке 9 диаграмму знаков второй производной y" (x)
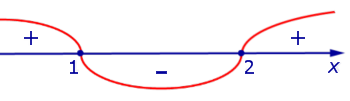
Рис.9
При переходе через точку x = 1 вторая производная функции y" (x) меняет знак с «+» на «–» . Следовательно, x = 1 – точка перегиба графика функции.
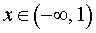При переходе через точку x = 2 вторая производная функции y" (x) меняет знак с «–» на «+» . Следовательно, x = 2 также является точкой перегиба графика функции.
При 
и при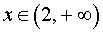 
вторая производная функции y" (x) > 0, следовательно, функция y (x) выпукла вниз на этих интервалах.
При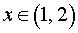 
вторая производная функции y" (x) < 0, следовательно, функция y (x) выпукла вверх на интервале (1, 2) .
Близкие по тематике разделы сайта
С материалами, связанными с дифференцированием функций и применением производных к исследованию поведения функций, можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»
Исследование функций с помощью производных и примеры построения графиков функций можно посмотреть в учебных пособиях:
- «Исследование функций с помощью производных. Построение графиков (часть 1)»
- «Исследование функций с помощью производных. Построение графиков (часть 2)»
на странице «Учебные материалы по математическому анализу для студентов МФТИ (1 курс, 1 семестр)».