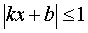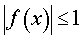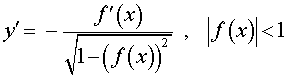Справочник по математике Элементы математического анализа
Элементы математического анализа Производная функции
Производная функции
Правила вычисления производных. Таблица производных часто встречающихся функций. Таблица производных сложных функций
Содержание
 |
Правила вычисления производных |
 |
Таблица производных часто встречающихся функций |
 |
Таблица производных сложных функций |

Правила вычисления производных
Вычисление производных основано на применении следующих правил, которые мы будем использовать без доказательств, поскольку доказательства выходят за рамки школьного курса математики.
ПРАВИЛО 1 (производная от произведения числа на функцию). Справедливо равенство
(c f (x))' = c f ' (x) ,
где c – любое число.
Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.
ПРАВИЛО 2 (производная суммы функций). Производная суммы функций вычисляется по формуле
(f (x) + g (x))' = f ' (x) + g' (x),
то есть производная от суммы функций равна сумме производных этих функций.
ПРАВИЛО 3 (производная разности функций). Производная разности функций вычисляется по формуле
(f (x) – g (x))' = f ' (x) – g' (x),
то есть производная от разности функций равна разности производных этих функций.
ПРАВИЛО 4 (производная произведения двух функций). Производная произведения двух функций вычисляется по формуле
(f (x) g (x))' = f ' (x) g (x) + f (x) g' (x),
Другими словами, производная от произведения двух функций равна производной от первой функции, умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.
ПРАВИЛО 5 (производная частного двух функций). Производная от дроби (частного двух функций) вычисляется по формуле
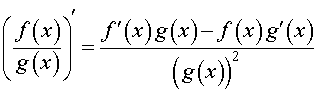
ОПРЕДЕЛЕНИЕ. Рассмотрим функции f (x) и g (x) . Сложной функцией или «функцией от функции» называют функцию вида
f (g (x))
При этом функцию f (x) называют внешней функцией, а функцию g (x) – внутренней функцией.
ПРАВИЛО 6 (производная сложной функции). Производная сложной функции вычисляется по формуле
[ f (g (x))]' = f ' (g (x)) g' (x)
Другими словами, для того, чтобы найти производную от сложной функции f (g (x)) в точке x нужно умножить производную внешней функции, вычисленную в точке g (x) , на производную внутренней функции, вычисленную в точке x .
Таблица производных часто встречающихся функций
В следующей таблице приведены формулы для производных от степенных, показательных (экспоненциальных), логарифмических, тригонометрических и обратных тригонометрических функций. Доказательство большинства их этих формул выходит за рамки школьного курса математики.
| Производная от постоянной функции |
|
Функция: y = c , где c – любое число Формула для производной: y' = 0 |
| Производная степенной функции |
|
Функция: y = x c , где c – любое число Формула для производной: y' = c xc – 1 |
| Производная от экспоненты (показательной функции с основанием e) |
|
Функция: y = e x Формула для производной: y' = e x |
| Производная от показательной функции с основанием a |
|
Функция: y = a x где a – любое положительное число, не равное 1 Формула для производной: y' = a x ln a |
| Производная от натурального логарифма |
|
Функция: y = ln x , x > 0 Формула для производной: 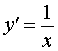 , x > 0 , x > 0 |
| Производная от логарифма по основанию a |
|
Функция: y = log a x , x > 0 где a – любое положительное число, не равное 1 Формула для производной: 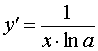 , x > 0 , x > 0 |
| Производная синуса |
|
Функция: y = sin x Формула для производной: y' = cos x |
| Производная косинуса |
|
Функция: y = cos x Формула для производной: y' = – sin x |
| Производная тангенса |
|
Функция: y = tg x , где
Формула для производной: 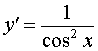 , ,
|
| Производная котангенса |
|
Функция: y = ctg x , где 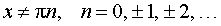
Формула для производной:
|
| Производная арксинуса |
|
Функция: y = arcsin x , Формула для производной: 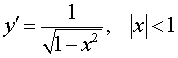 |
| Производная арккосинуса |
|
Функция: y = arccos x , Формула для производной: 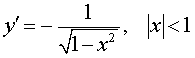 |
| Производная арктангенса |
|
Функция: y = arctg x Формула для производной: 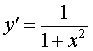 |
| Производная арккотангенса |
|
Функция: y = arcctg x Формула для производной: 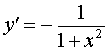 |
Таблица производных сложных функций
В следующей таблице приведены формулы для производных сложных функций.
В отдельных строках (с голубым фоном) приведены формулы для производных сложных функций в случае, когда внутренняя функция является линейной функцией и имеет вид f (x) = kx + b , где k и b – любые числа, 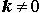 .
.
|
Функция: y = (kx + b) c , где c – любое число. Формула для производной: y' = kc (kx + b) c – 1 , |
|
Функция: y = ( f (x)) c , где c – любое число. Формула для производной: 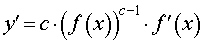 |
|
Функция: y = ekx + b Формула для производной: |
|
Функция: y = e f (x) Формула для производной: 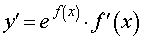 |
|
Функция: y = akx + b где a – любое положительное число, не равное 1 Формула для производной: 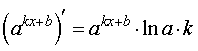 |
|
Функция: y = a f (x) где a – любое положительное число, не равное 1 Формула для производной: 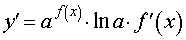 |
|
Функция: y = ln (kx + b) , kx + b > 0 Формула для производной:
|
|
Функция: y = ln ( f (x)) , f (x) > 0 Формула для производной:
|
|
Функция: y = log a (kx + b) , kx + b > 0 где a – любое положительное число, не равное 1 Формула для производной: 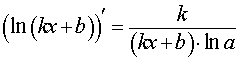 , kx + b > 0 , kx + b > 0 |
|
Функция: y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1 Формула для производной: 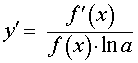 , f (x) > 0 , f (x) > 0 |
|
Функция: y = sin (kx + b) Формула для производной: y' = k cos (kx + b) |
|
Функция: y = sin ( f (x)) Формула для производной: |
|
Функция: y = cos (kx + b) Формула для производной: y' = – k sin (kx + b) |
|
Функция: y = cos ( f (x)) Формула для производной: 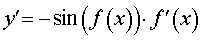 |
|
Функция: y = tg (kx + b), где Формула для производной: 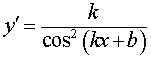 , , 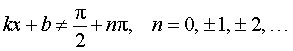 |
|
Функция: y = tg ( f (x)), где Формула для производной: 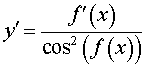 , , 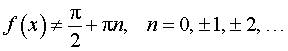 |
|
Функция: y = ctg (kx + b), где Формула для производной: 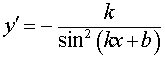 , , 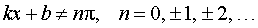 |
|
Функция: y = ctg ( f (x)), где Формула для производной: 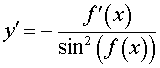 , , 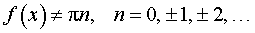 |
|
Функция: y = arcsin (kx + b), Формула для производной: 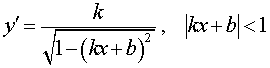 |
|
Функция: y = arcsin ( f (x)), Формула для производной: 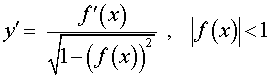 |
|
Функция: y = arccos (kx + b), Формула для производной: 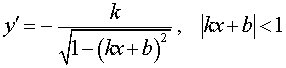 |
|
Функция: y = arccos ( f (x)), Формула для производной:
|
|
Функция: y = arctg (kx + b) Формула для производной: 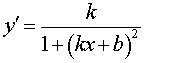 |
|
Функция: y = arctg ( f (x)) Формула для производной: 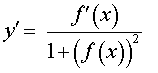 |
|
Функция: y = arcctg (kx + b) Формула для производной: 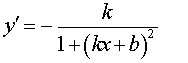 |
|
Функция: y = arcctg ( f (x)) Формула для производной: 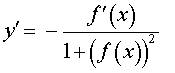 |
Близкие по тематике разделы сайта
С материалами, связанными с дифференцированием функций и применением производных к исследованию поведения функций, можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»
Исследование функций с помощью производных и примеры построения графиков функций можно посмотреть в учебных пособиях:
- «Исследование функций с помощью производных. Построение графиков (часть 1)»
- «Исследование функций с помощью производных. Построение графиков (часть 2)»
на странице «Учебные материалы по математическому анализу для студентов МФТИ (1 курс, 1 семестр)».

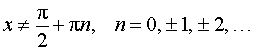
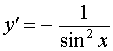 ,
,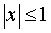
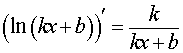 , kx + b > 0
, kx + b > 0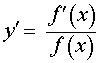 , f (x) > 0
, f (x) > 0