Логарифмы
Определение логарифма, основное логарифмическое тождество
Рассмотрим два произвольных действительных числа a и b, удовлетворяющих условиям
| (1) |
Определение. Логарифмом числа b по основанию a называют такую степень, в которую надо возвести число a, чтобы получить число b.
Другими словами, логарифм числа b по основанию a – это такое число x, которое является решением уравнения
| a x= b . | (2) |
Доказательство того, что решение уравнения (2) существует и единственно, выходит за рамки школьной программы.
Для логарифма числа b по основанию a используется обозначение:
loga b .
Таким образом, для всех действительных чисел a и b, удовлетворяющих условиям (1), справедливо равенство
![]()
которое часто называют основным логарифмическим тождеством.
Замечание. Обратим особое внимание на то, что при решении уравнения (2) мы ищем показатель степени, а при решении уравнения
x a = b.
мы ищем основание степени, которое вычисляется по формуле
![]()
и в случае, когда a – натуральное число, является корнем натуральной степени из числа b.
Пример 1. Решить уравнение
x3 = 81 .
Решение. Воспользовавшись понятием кубического корня и свойствами степеней, получаем
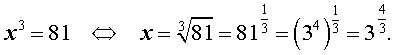
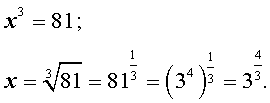
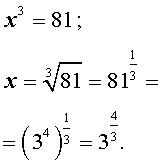
Ответ: ![]() .
.
Пример 2. Решить уравнение
3x= 81 .
Решение. Воспользовавшись тем, что число 81 является четвертой степенью числа 3 , получаем:
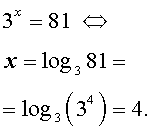
Ответ: 4 .
Задача. Доказать, что число
log2 3
Решение. Предположим противное, т.е. предположим, что указанное число рационально. Тогда существует несократимая дробь
![]() ,
,
числитель и знаменатель которой являются натуральными числами и такая, что справедливо равенство:
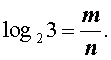
Из определения логарифма отсюда вытекает равенство:
![]()
следствием которого является равенство:
2m= 3n .
Но последнее равенство невозможно, поскольку его левая часть четное число, а правая – нечетное. Полученное противоречие доказывает требуемое в задаче утверждение.
Свойства логарифмов
Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:
 | |
 | |
 | |
 | 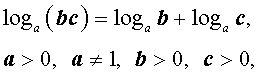 (основное свойство логарифмов), |
 | 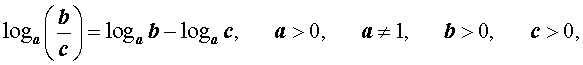 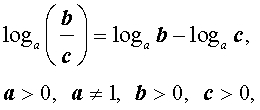 (основное свойство логарифмов), |
 | 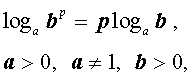 |
 | 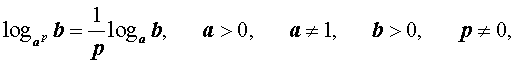 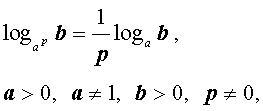 |
 | 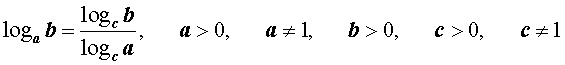 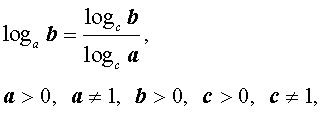 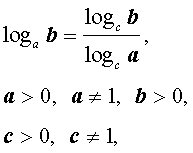 (формула перехода к новому основанию логарифмов), |
 | 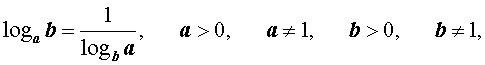 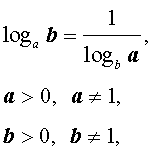 |
 | 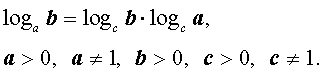 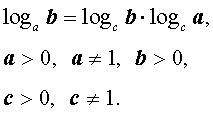 |
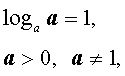 |
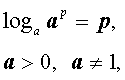 |
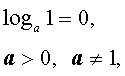 |
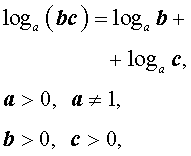 (основное свойство логарифмов), |
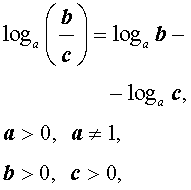 (основное свойство логарифмов), |
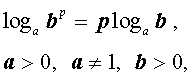 |
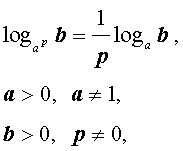 |
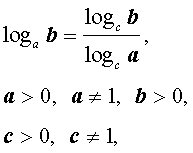 (формула перехода к новому основанию логарифмов), |
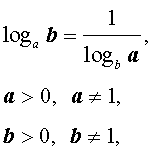 |
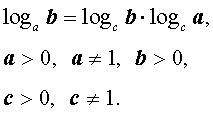 |
Использование свойств логарифмов при решении логарифмических уравнений и неравенств
Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.
Например, если при решении уравнения или неравенства требуется преобразовать выражение
loga ( f (x)2 ) ,
то вместо формулы
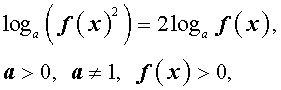
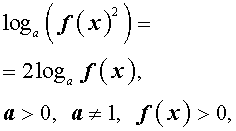
следует применять формулу
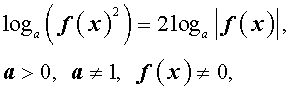
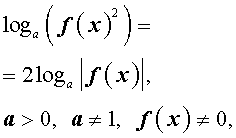
поскольку в противном случае можно потерять корни.
По той же причине при преобразовании выражений
loga ( f (x) g (x)) и 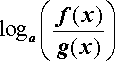
следует использовать формулы:
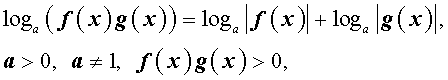
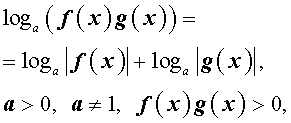
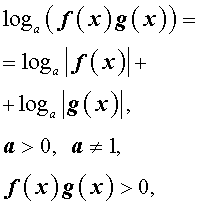
и
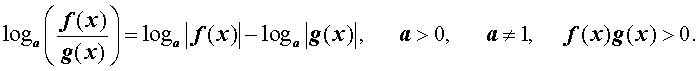
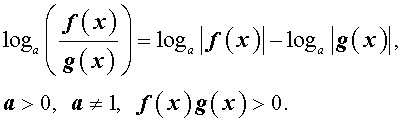
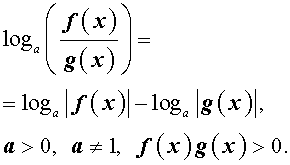
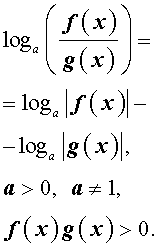
Замечание. Желающим усовершенствовать свои знания и умения при решении уравнений и неравенств с логарифмами мы рекомендуем ознакомиться с нашими учебными пособиями «Решение логарифмических уравнений» и «Решение логарифмических неравенств».
Десятичные логарифмы и натуральные логарифмы
В математике, физике и во многих других областях естествознания и технологий важное место занимают десятичные логарифмы и натуральные логарифмы.
Десятичные логарифмы – это логарифмы с основанием 10, а основанием натуральных логарифмов является иррациональное и трансцендентное число e, которое определяется по формуле
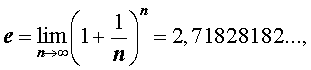
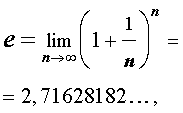
доказательство которой выходит за рамки школьной программы.
Для десятичных и натуральных логарифмов используются соответственно обозначения:
lg b и ln b,
причем
lg e = 0,43429…,
ln 10 = 2,30259…
Графики логарифмических функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
