Арифметико-геометрическая прогрессия
 Определение арифметико-геометрической прогрессии Определение арифметико-геометрической прогрессии |
 Вывод формулы для общего члена арифметико-геометрической прогрессии Вывод формулы для общего члена арифметико-геометрической прогрессии |
Определение арифметико-геометрической прогрессии
Рассмотрим более сложный, чем арифметическая или геометрическая прогрессии, тип последовательности чисел. Эта последовательность носит название арифметико-геометрической прогрессии, поскольку обладает рядом свойств, присущих, как арифметической, так и геометрической прогрессиям.
Определение. Арифметико-геометрической прогрессией называют числовую последовательность
x1 , x2 , … xn , …
заданную рекуррентной формулой
| xn = q xn – 1 + d , n > 1 | (1) |
с начальным условием
| x1 = c1 , | (2) |
где буквами
q , d , c1 ,
обозначены заданные числа, удовлетворяющие условиям
| (3) |
Замечание. Условия (3) входят в определение, поскольку при q = 1 арифметико–геометрическая прогрессия превращается в арифметическую прогрессию, а при d = 0 арифметико–геометрическая прогрессия превращается в геометрическую прогрессию.
Вывод формулы общего члена арифметико-геометрической прогрессии
Перейдем от последовательности
x1 , x2 , … xn , …
к последовательности
y1 , y2 , … yn , …
по формулам
| xn = yn + t , | (4) |
где t – некоторое число, которое мы определим чуть позже.
Поскольку
xn – 1 = yn – 1 + t ,
то формула (1) преобразуется следующим образом:
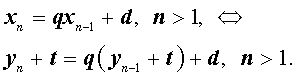
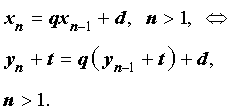
Следовательно,
| yn = q yn – 1 + + ( q – 1) t + d , n > 1 . | (5) |
Если теперь положить
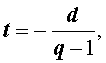 | (6) |
то формула (5) принимает вид
| yn = q yn – 1 , n > 1 , | (7) |
откуда вытекает, что последовательность
y1 , y2 , … yn , …
является геометрической прогрессией со знаменателем q.
Для того, чтобы найти первый член этой геометрической прогрессии, воспользуемся равенствами (2) и (4):
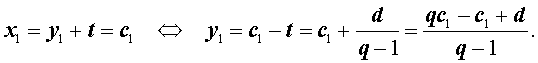
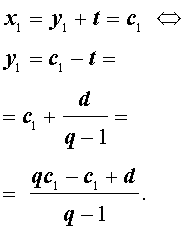
Итак,
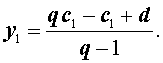 | (8) |
Поскольку
yn = y1q n – 1,
то из формул (7) и (8) получаем формулу для общего члена геометрической прогрессии (7):
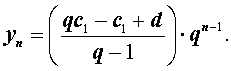 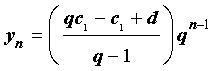 | (9) |
Из формулы (9) с помощью равенств (4) и (6) получаем формулу общего члена арифметико-геометрической прогрессии:
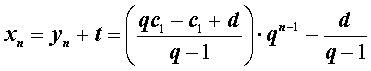
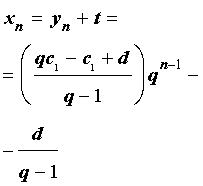
Итак, формула общего члена арифметико-геометрической прогрессии имеет вид:
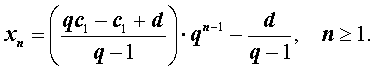
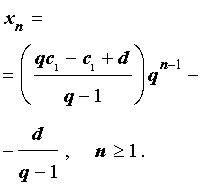
Вывод формулы общего члена закончен.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
