Справочник по математике

Геометрия (Стереометрия)

Прямые и плоскости в пространстве

Взаимное расположение двух плоскостей в пространстве.
Признаки параллельности двух плоскостей

Признаки параллельности плоскостей

      Две плоскости в пространстве могут быть параллельными или могут пересекаться, как показано в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся плоскости		Две плоскости называют пересекающимися, если они не совпадают, и у них есть общие точки. В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия.
Две параллельные плоскости		Две плоскости называют параллельными, если они не имеют общих точек.

Две пересекающиеся плоскости

Определение: Две плоскости называют пересекающимися, если они не совпадают, и у них есть общие точки. В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия.

Две параллельные плоскости

Определение: Две плоскости называют параллельными, если они не имеют общих точек.

Признаки параллельности двух плоскостей

      Первый признак параллельности двух плоскостей. Если две пересекающиеся прямые пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

      Доказательство. Рассмотрим рисунок 1, на котором изображены плоскости  α  и   β

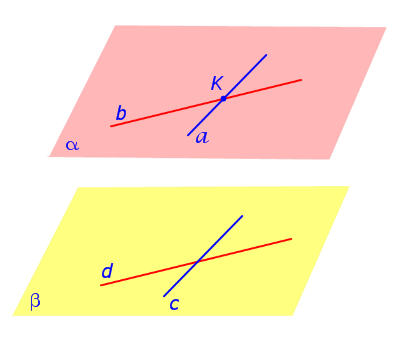
Рис.1

      Прямые a и b лежат в плоскости  α  и пересекаются в точке K. Прямые c и d лежат в плоскости  β  и параллельны прямым a и b соответственно.

      Будем доказывать первый признак параллельности двух плоскостей методом «от противного». Для этого предположим, что плоскости  α  и   β  не параллельны. Следовательно, плоскости  α  и   β  должны пересекаться, причём пересекаться по некоторой прямой. Обозначим прямую линию, по которой пересекаются плоскости  α  и   β  буквой l (рис.2) и воспользуемся признаком параллельности прямой и плоскости.

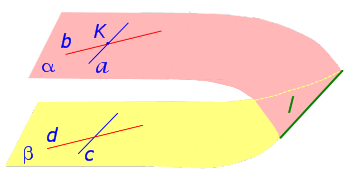
Рис.2

      Плоскость  α  проходит через прямую a, параллельную прямой c, и пересекает плоскость   β  по прямой l. Отсюда, в силу признака параллельности прямой и плоскости, заключаем, что прямые a и l параллельны. В то же время плоскость  α  проходит через прямую b, параллельную прямой d, и пересекает плоскость  β  по прямой l. Отсюда, в силу признака параллельности прямой и плоскости, заключаем, что прямые b и l параллельны. Таким образом, мы получили, что на плоскости  α  через точку K проходят две прямые, а именно, прямые a и b, которые параллельны прямой l. Полученное противоречие с аксиомой о параллельных прямых аксиомой о параллельных прямых даёт возможность утверждать, что предположение о том, что плоскости  α  и   β  пересекаются, является неверным. Доказательство первого признака параллельности двух плоскостей завершено.

      Второй признак параллельности двух плоскостей. Если две пересекающиеся прямые, лежащие в одной плоскости, параллельны другой плоскости, то такие плоскости параллельны.

      Доказательство. Рассмотрим рисунок 3, на котором изображены плоскости  α  и   β.

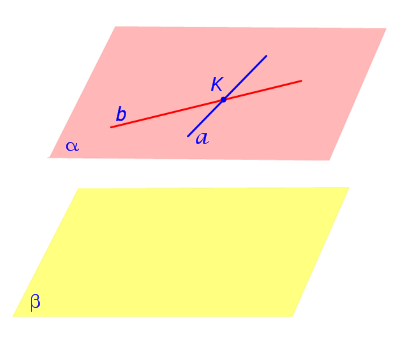
Рис.3

      На этом рисунке также изображены прямые a и b, которые лежат в плоскости  α  и пересекаются в точке K. По условию каждая из прямых a и b параллельна плоскости  β. Требуется доказать, что плоскости  α  и   β  параллельны.

      Доказательство этого утверждения аналогично доказательству первого признака параллельности двух плоскостей, и мы  его оставляем читателю в качестве полезного упражнения.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ по математике.