Решение рациональных неравенств. Метод интервалов
Определение. Рациональным неравенством называют такое неравенство, которое при помощи равносильных преобразований сводится к одному из следующих неравенств
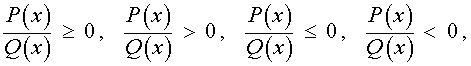
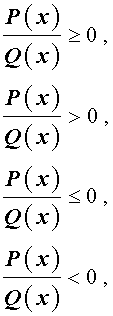
где P(x) и Q(x) – многочлены.
Для решения рациональных неравенств часто используют удобный способ, который получил название «метод интервалов». Продемонстрируем применение метода интервалов на примерах.
Пример 1. Решить неравенство
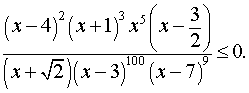 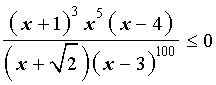 | (1) |
Решение. Вводя обозначение
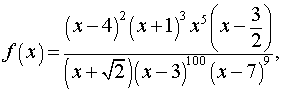 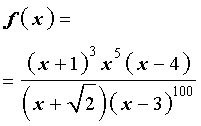 | (2) |
перепишем неравенство (1) в виде
| (3) |
Заметим, что и числитель, и знаменатель дроби из правой части формулы (2) являются произведением выражений типа
| (x – a)k, | (4) |
где a – вещественное число, а k – натуральное число. Действительно, произведение выражений
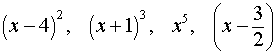 | (5) |
равно числителю дроби (2), а произведение выражений
| (6) |
равно знаменателю дроби (2).
В случае, когда показатель степени k в формуле (4) является нечётным числом, выражение (4) отрицательно для всех значений x, лежащих на числовой оси слева от числа a, и положительно для всех значений x, лежащих на числовой оси справа от числа a.
В случае, когда показатель степени k в формуле (4) является чётным числом, выражение (4) положительно для всех значений x, отличных от числа a.
Следовательно, если отметить на числовой оси числа
| (7) |
играющие роль числа a из формулы (4) в выражениях (5), а также отметить на числовой оси числа
| (8) |
играющие роль числа a из формулы (4) в выражениях (6), то внутри каждого из промежутков, полученных на числовой оси, функция (2) будет сохранять свой знак. Другими словами, внутри каждого из полученных промежутков числовой оси значения функции (2) будут или положительными, или отрицательными.
Для того, чтобы воспользоваться этим рассуждением, отметим на числовой оси в нужном порядке числа (7) и (8), причём числа (7) изобразим закрашенными кружками, а числа (8) – незакрашенными кружками (рис.1).
  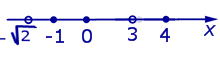 |
| Рис.1 |
Перейдём от рисунка 1 к рисунку 2.
  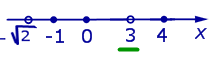 |
| Рис.2 |
На рисунке 2 подчёркнуты числа 3 и 4, то есть те из чисел (7) и (8), которым соответствуют чётные показатели степени в выражениях (5) и (6). Действительно, числам 3 и 4 соответствуют чётные показатели степени в выражениях (5) и (6)подчёркнуто число 3, то есть то из чисел (7) и (8), которому соответствует чётный показатель степени в выражениях (5) и (6). Действительно, числу 3 соответствует чётный показатель степени в выражении (6), поскольку числу 3 соответствует выражение
(x – 3 )100
с показателем степени 100, а числу 4 соответствует выражение.
(x – 4 )2
с показателем степени 2 .
Нанесем на рисунок 2 волновую линию, начиная от правого верхнего угла рисунка и двигаясь влево (рис.3) .
  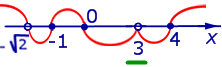 |
| Рис.3 |
Мы начинаем вести волновую линию от правого верхнего угла рисунка, поскольку справа от всех точек (7) и (8) функция (2) принимает положительные значения.
Заметим, что волновая линия на рисунке (3) вблизи от подчёркнутых точек 3 и 4подчёркнутой точки 3 располагается по одну сторону от числовой оси, а в точках
| (9) |
которым соответствуют нечётные показатели степени в выражениях (5) и (6), пересекает числовую ось и вблизи от этих точек располагается по разные стороны от числовой оси.
Важно отметить, что значения функции (2) внутри каждого из промежутков имеют один и тот же знак. При переходе от промежутка к соседнему промежутку через точки (9), которым соответствуют нечётные показатели степени в выражениях (5) и (6), значения функции (2) меняют знак на противоположный. При переходе от промежутка к соседнему промежутку через точки 3 и 4, которым соответствуют чётные показателиточку 3, которой соответствует чётный показатель степени в выражениях (5) и (6), значения функции (2) знак не изменяют.
Нанесем на рисунок 3 знаки « + » и « – », как показано на рисунке 4.
  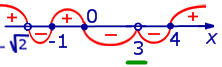 |
| Рис.4 |
На промежутках, отмеченных знаком « + », функция (2) принимает положительные значения. На промежутках, отмеченных знаком « – », функция (2) принимает отрицательные значения. Отсюда вытекает, что решением неравенства (1) является объединение промежутков, отмеченных знаком « – », поскольку именно на этих промежутках функция (2) принимает отрицательные значения. Для завершения решения примера остаётся лишь добавить, что концы промежутков
отмеченные на рисунках закрашенными кружками, входят в ответ задачи, а концы промежутков
отмеченные на рисунках незакрашенными кружками, не входят в ответ задачи.
Ответ:
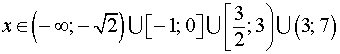
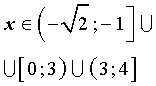
Пример 2. Решить неравенство
| (10) |
Решение. Преобразуем неравенство (10) к такому виду, чтобы можно было применить метод интервалов:
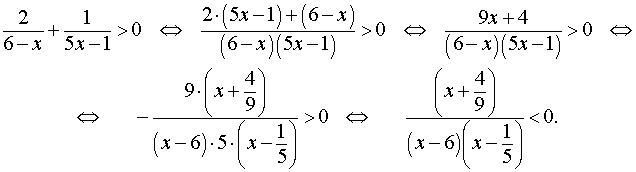
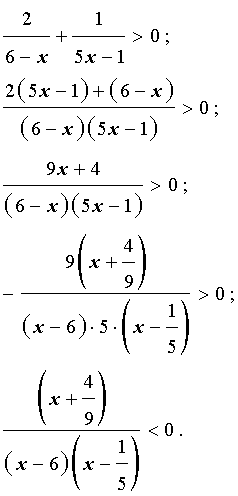
Неравенство
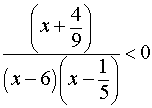 | (11) |
имеет вид (1). Решим его методом интервалов. Для этого отметим незакрашенными кружками числа
![]()
  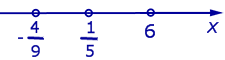 |
| Рис.5 |
Проведём волну, начиная движение от правого верхнего угла, и отметим знаками « + » и « – » промежутки числовой оси (рис.6)
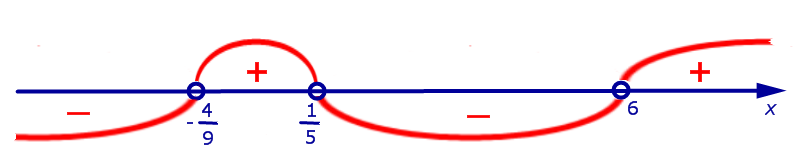   |
| Рис.6 |
Решением неравенства (11) являются промежутки, отмеченные знаком « – » . Концы промежутков в ответ не входят.
Ответ: 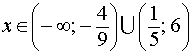
Замечание. Рекомендуем ознакомиться с нашим учебным пособием «Решение рациональных неравенств», близко связанным с материалом данного раздела справочника.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
