Занятия будут проходить 1 раз в неделю по 90 минут

Подробности по телефону   (495) 509-28-10

Нам не все равно, как Вы сдадите экзамены!

А Вам?

Справочник по математике

Геометрия (Планиметрия)

Углы

Теорема Фалеса

      Теорема Фалеса. Через произвольные точки

A₁,  A₂,  …   A_n–1,  A_n,

лежащие на стороне AO угла AOB (рис.1), проведены параллельные прямые, пересекающие сторону угла OB в точках

B₁,  B₂,  …  B_n–1,  B_n,

соответственно. Тогда справедливы равенства

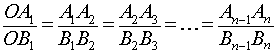
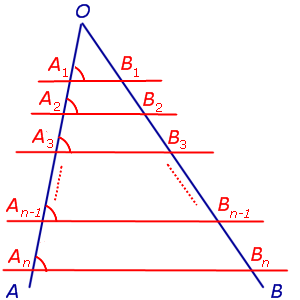
Рис.1

      Доказательство. Докажем сначала следующую лемму.

      Лемма. Через произвольную точку C, лежащую на стороне OA треугольника OAB, проведена прямая, параллельная прямой AB и пересекающая сторону OB в точке D (рис.2).

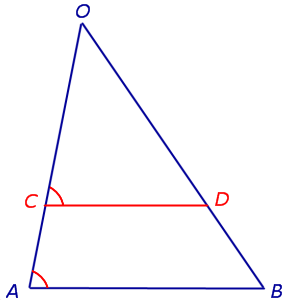
Рис.2

      Тогда справедливо равенство

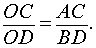(1)

      Доказательство леммы. Опустим из точек A и B перпендикуляры AK и BL на прямую CD (рис.3). Заметим, что эти перпендикуляры равны, поскольку AKLB – прямоугольникпрямоугольник.

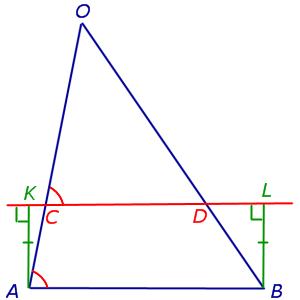
Рис.3

      Из точки D опустим перпендикуляр DF на прямую OA (рис.4).

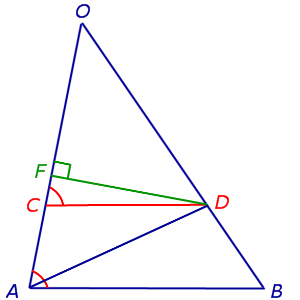
Рис.4

      Из точки C  опустим перпендикуляр CG на прямую OB (рис.5).

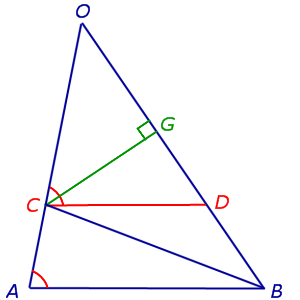
Рис.5

      В соответствии с рисунком 4 площади треугольников OCD и ACD можно вычислить по формулам

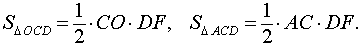
      Следовательно,

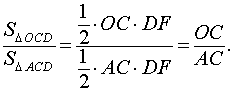
      В соответствии с рисунком 5 площади треугольников OCD и BCD можно вычислить по формулам

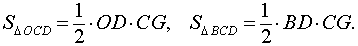
      Следовательно,

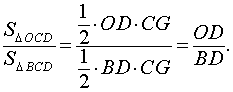
      Кроме того, заметим, что площади треугольников ACD и BCD равны. Действительно, в соответствии с рисунком 3 справедливы формулы

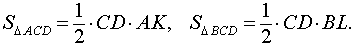
      Следовательно,

S_{Δ ACD} = S_{Δ BCD} ,

откуда получаем цепочку равенств

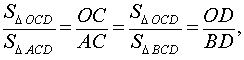
что и завершает доказательство леммы.

      Воспользовавшись леммой, заметим (рис.1), что из равенства (1) вытекают равенства

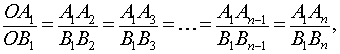
откуда на основе свойств производных пропорций, заключаем, что справедливы равенства

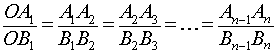
что и завершает доказательство теоремы Фалеса.

      Следствие. Если через точки

A₁,  A₂,  …   A_n–1,  A_n,

лежащие на стороне AO угла AOB (рис.6) и удовлетворяющие условию

A₁A₂ = A₂A₃ = … =
= A_n–2 A_n–1 = A_n–1A_n ,

проведены параллельные прямые, пересекающие сторону угла OB в точках

B₁, B₂,  …   B_{n –1},  B_n ,

соответственно, то справедливы равенства

B₁B₂ = B₂B₃ = … =
= B_n–2B_n–1 = B_n–1B_n ,

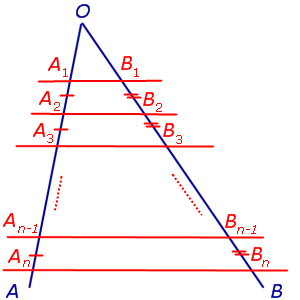
Рис.6

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

подготовительные курсы для школьников 8, 9, 10 и 11 классов

      У нас также для школьников организованы

индивидуальные занятия с репетиторами по математике и русскому языку

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»