Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Треугольники
Треугольники
Свойства сторон и углов треугольника
| Определение треугольника |
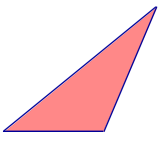
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Определение Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков – вершинами треугольника. |
| Свойство большей стороны треугольника |
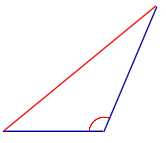
Свойство Против большей стороны треугольника лежит больший угол |
| Свойство большего угла треугольника |

Свойство Против большего угла треугольника лежит большая сторона |
| Свойство меньшей стороны треугольника |
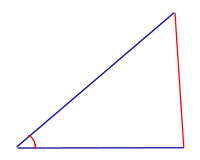
Свойство Против меньшей стороны треугольника лежит меньший угол |
| Свойство меньшего угла треугольника |

Свойство Против меньшего угла треугольника лежит меньшая сторона |
| Неравенства треугольника |
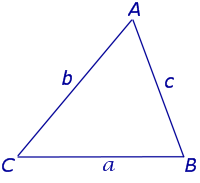
Неравенства треугольника Длина любой стороны треугольника меньше суммы длин двух других сторон. a < b + c Длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| |
| Свойство углов треугольника |
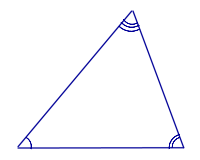
Свойство Сумма углов треугольника равна 180° |
| Свойство внешнего угла треугольника |
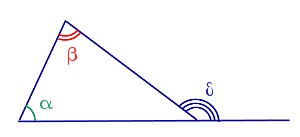
Свойство Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ = α + β . |
| Свойство большего угла треугольника |
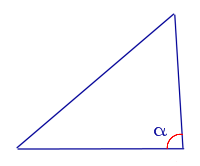
Свойство Величина большего угла треугольника не может быть меньшей, чем 60°.
где α – больший угол треугольника. |
| Свойство меньшего угла треугольника |
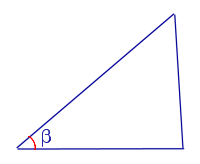
Свойство Величина меньшего угла треугольника не может быть большей, чем 60°.
где β – меньший угол треугольника. |
| Теорема косинусов |
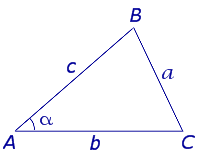
Теорема косинусов a2 = b 2 + c 2 – 2bc cos α , |
| Теорема синусов |
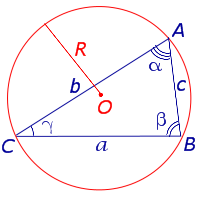
Теорема синусов
где R – радиус описанной окружности. |

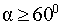
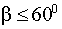
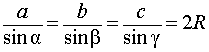 ,
,