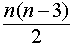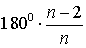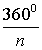Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Многоугольники
Многоугольники
Многоугольники
Содержание

Определение многоугольника
Рассмотрим n отрезков
| [A1 A2], [A2 A3], … , [An An +1] | (1) |
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).
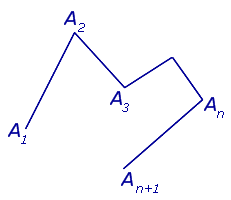
Рис. 1
ОПРЕДЕЛЕНИЕ 1. Ломаной линией с n звеньями называют фигуру L, составленную из отрезков (1), то есть фигуру, заданную равенством
L = [A1 A2] U [A2 A3] U … U [An An +1]
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).
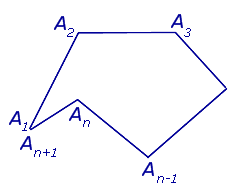
Рис. 2
ОПРЕДЕЛЕНИЕ 2. Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию (звенья), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.
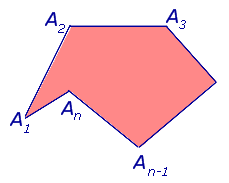
Рис. 3
ОПРЕДЕЛЕНИЕ 3. Многоугольник называют n – угольником, если он имеет n сторон.
Таким образом, многоугольник, имеющий 3 стороны, называют треугольником, многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.
ОПРЕДЕЛЕНИЕ 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.
Величину, равную половине периметра, называют полупериметром.
Диагонали n - угольника
| Определение диагонали многоугольника |
|
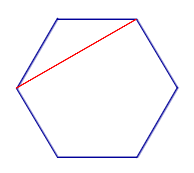
Определение Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Свойство диагоналей многоугольника, выходящих из одной вершины |
|
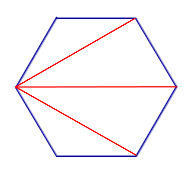
Свойство Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Число диагоналей многоугольника |
|
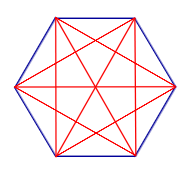
Число диагоналей n – угольника равно
|
Внешний угол многоугольника
ОПРЕДЕЛЕНИЕ 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).

Рис.1
ОПРЕДЕЛЕНИЕ 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
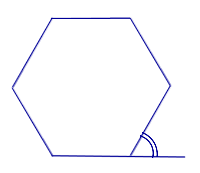
Рис.2
ЗАМЕЧАНИЕ. Мы рассматриваем только выпуклые многоугольники.
Свойства углов треугольника
| Свойство углов треугольника |
|
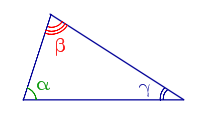
Свойство Сумма углов треугольника равна 180° α + β + γ = 180° |
| Свойство внешнего угла треугольника |
|
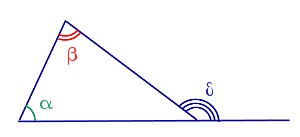
Свойство Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним δ = α + β |
Свойства углов многоугольника
| Свойство углов n – угольника |
|
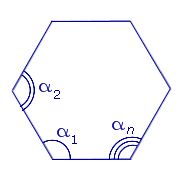
Свойство Сумма углов многоугольника равна
|
| Свойство внешних углов n – угольника |
|
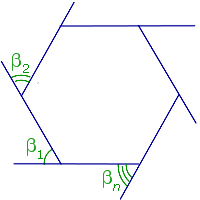
Свойство Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° |
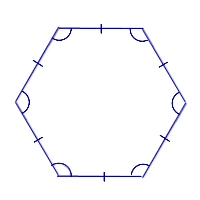
Свойства углов правильного n – угольника
| Свойство углов правильного n – угольника |
|
Свойство Все углы правильного n – угольника равны
|
| Свойство внешних углов правильного n – угольника |
|
Свойство Все внешние углы правильного n – угольника равны
|
Доказательства свойств углов многоугольника
ТЕОРЕМА 1. В любом треугольнике сумма углов равна 180°.
ДОКАЗАТЕЛЬСТВО. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
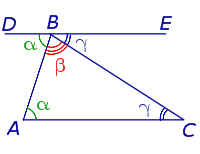
Рис.3
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.
ТЕОРЕМА 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
ДОКАЗАТЕЛЬСТВО. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
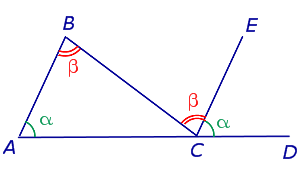
Рис.4
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные. Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.
ЗАМЕЧАНИЕ. Теорема 1 является следствием теоремы 2.
ТЕОРЕМА 3. Сумма углов n – угольника равна
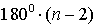
ДОКАЗАТЕЛЬСТВО. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
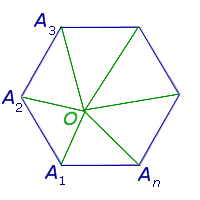
Рис.5
Получим n треугольников:
OA1A2, OA2A3, … OAnA1
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна
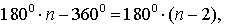
что и требовалось доказать.
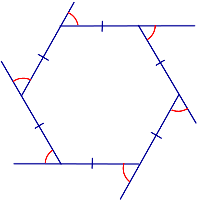
ТЕОРЕМА 4. Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°.
ДОКАЗАТЕЛЬСТВО. Рассмотрим рисунок 6.
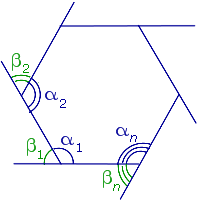
Рис.6
В соответствии рисунком 6 справедливы равенства
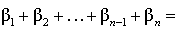
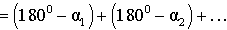
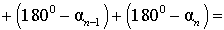
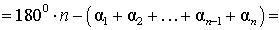
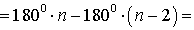
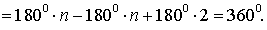
Теорема доказана.