Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Четырехугольники
Четырехугольники
Описанные четырехугольники
ОПРЕДЕЛЕНИЕ 1. Окружностью, вписанной в четырёхугольник, называют окружность, которая касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником.

Рис.1
ЗАМЕЧАНИЕ. В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.
ТЕОРЕМА 1. Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.
ДОКАЗАТЕЛЬСТВО. Рассмотрим четырёхугольник ABCD, описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис.2).
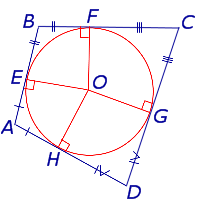
Рис.2
В силу теоремы об отрезках касательных, проведённых к окружности из одной точки, справедливы равенства
AH = AE, BF = BE, CF = CG, DH = DG,
Складывая эти равенства, получим:
AH + BF + CF + DH = AE + BE + CG + DG,
Поскольку
AH + BF + CF + DH = AD + BC,
AE + BE + CG + DG = AB + CD,
то справедливо равенство
AD + BC = AB + CD,
что и требовалось доказать.
ТЕОРЕМА 2 (обратная теорема к теореме 1). Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.
ДОКАЗАТЕЛЬСТВО. Рассмотрим четырёхугольник ABCD, длины сторон которого удовлетворяют равенству
AD +BC = AB + CD,
и проведём биссектрисы углов BAD и CDA. Обозначим точку пересечения этих биссектрис буквой O, и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).
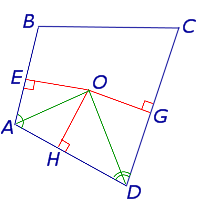
Рис.3
Поскольку точка O лежит на биссектрисе угла BAD, то справедливо равенство
OH = OE,
Поскольку точка O лежит на биссектрисе угла ADC, то справедливо равенство
OH = OG,
Следовательно, справедливы равенства
OH = OE = OG,
из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH, касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:
-
Окружность касается стороны BC (рис.4).
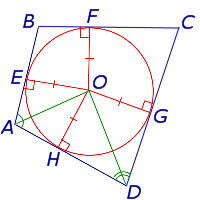
Рис.4
В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.
-
Окружность не касается стороны BC.
В этом случае касательная, проведенная к окружности из точки B, пересекает прямую DC в точке K, и возможны два случая:
-
Точка K лежит между точками C и D (рис.5)
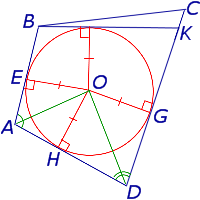
Рис.5
- Точка C лежит между точками K и D (рис.6)
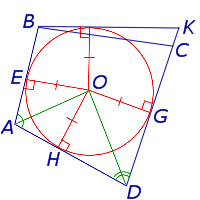
Рис.6
-
Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:
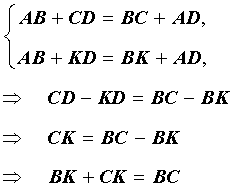
Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольника. Полученное противоречие доказывает, что случай 2а невозможен.
Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.
Итак, возможен и реализуется лишь случай 1.
Теорема доказана.
Из доказательства теоремы 2 непосредственно вытекает
ТЕОРЕМА 3. Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.
В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.
ПРИМЕРЫ ОПИСАННЫХ ЧЕТЫРЕХУГОЛЬНИКОВ
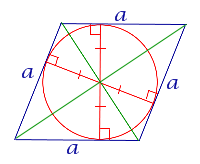
| Ромб |
|
|
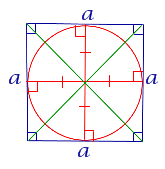
| Квадрат |
|
В любой квадрат можно вписать окружность |
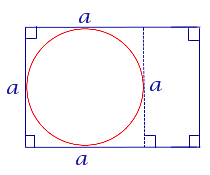
| Прямоугольник |
|
В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом |
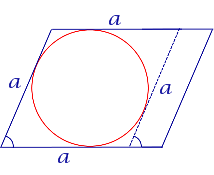
| Параллелограмм |
|
В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом |
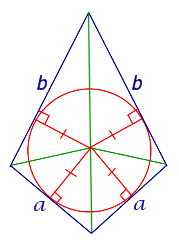
| Дельтоид |
|
|
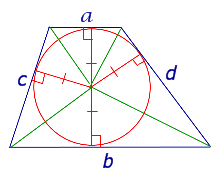
| Трапеция |
|
В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон равна сумме длин оснований |